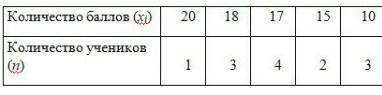
Найдите дисперсию и стандартное отклонение по имеющимся данным о распределений учащихся по количеству , полученных на Сор по математике
Другие вопросы по теме Алгебра
Популярные вопросы
- Велосипедист должен был проехать 60 км. В первый час он проехал 40% намеченного...
1 - Решить иррациональное уравнение.. всё под корнем )...
3 - Чим зумовлений цілющий ефект кордицепсу?...
1 - Цена книги 6 лари, что на 4 лари больше, чем цена тетради. Сколько стоит книга...
3 - Выпишете метафоры и найдите синонимы ОЧЕНЬ...
3 - Хочаб 3 відповідіПліз даю 20 б...
3 - я немогу сделать у меня СОР...
2 - Запишіть 2 ситуації, що врегульовуються нормами різних галузей права, й позначте...
1 - Решите Буду очень благодарен. У меня таких листов куча поэтому можете зайти...
3 - 3. Хлорид цинка является ионным соединением. (а) Укажите электронную конфигурацию...
2
Приведем очень простой пример, показывающий, как вычисляются дисперсия и стандартное отклонение. Допустим, что вам представилась возможность сыграть в следующую игру. Сначала вы инвестируете 100 уел. ед. Затем подбрасываете две монеты. Если выпадет “орел” — прибавляете к первоначальной сумме 20%, если “решка” — отнимаете 10%. Очевидно, существует четыре вероятных результата: “орел” + “орел”: +40%;
“орел” + “решка”: +10%;
“решка” + “орел”: +10%;
“решка” + “решка”: -20%.
Составим таблицу распределения частот:
X
+40
+10
-20
wt.
1
1
1
4
2
4
Относительная частота равна 1 к 4 (или 0,25), что вы получите 40%, равна 2 к 4 (или 0,5), что вы получите 10%, и 1 к 4 (или 0,25), что вы потеряете 20%. Ожидаемая доходность игры, следовательно, представляет собой средневзвешенную значений фактической доходности
Объяснение: