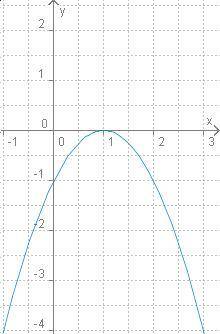
Найди по графику нули данной квадратичной функции.

Для того чтобы найти нули квадратичной функции по её графику, нужно определить точки, в которых график функции пересекает ось абсцисс (ось x). В этих точках y-координата будет равна 0.

В данном случае, на графике дана парабола, у которой ветви направлены вверх. Это свидетельствует о том, что функция является параболой вида f(x) = ax^2 + bx + c, где a > 0.

Нули функции соответствуют точкам, где график пересекает ось x. Из графика видно, что график пересекает ось x в двух точках: одна точка находится слева от вершины параболы, а вторая точка - справа от вершины параболы.

Первый ноль функции (x1) является отрицательным и находится слева от вершины. Чтобы его найти, рассмотрим ось симметрии параболы. Ось симметрии параболы проходит через вершину, поэтому x-координата вершины параболы будет равна x1. Таким образом, нужно найти x-координату вершины параболы.

На графике видно, что вершина параболы находится в точке с координатами (0, -2). Таким образом, x-координата вершины равна 0.

Теперь мы знаем, что x1 = 0. Каждая из нулей функции соответствует точке пересечения с осью x, поэтому первый ноль функции равен 0.

Второй ноль функции (x2) находится справа от вершины параболы. Поскольку график симметричен относительно оси симметрии, то x2 будет отрицательным.

На графике видим, что парабола пересекает ось x примерно в точке (-4, 0). Точное значение x2 можно найти путём решения квадратного уравнения f(x) = 0, где f(x) - заданная функция.

Итак, у нас есть функция f(x) = ax^2 + bx + c, где a, b и c - коэффициенты функции. Но у нас нет точных значений для этих коэффициентов, поэтому мы не можем решить это уравнение точно. Однако, мы можем приближённо найти значение x2.

Из графика видно, что x2 находится примерно на расстоянии -4 от вершины параболы. Таким образом, приближённое значение x2 равно -4.

Таким образом, нули данной квадратичной функции равны 0 и -4.