Напишите уравнение касательной к графику функции y=f(x) в точке с абсциссой x_0 1) f(x)=〖3x〗^2; x_0=2 2) f(x)=〖5x〗^2-3; x_0=-1
Другие вопросы по теме Алгебра
Популярные вопросы
- У скільки разів період обертання супутника, який рухається на висоті...
1 - ЛЖЕДМИТРИЙ 1 история РОССИИ 7 класс автор ПЧЕЛОВ И ЛУКИН краткое содержание...
1 - Используя метод электронного баланса, составьте уравнение реакции:...
2 - Речовин, структури сн.CHсH, Brму параграфi.64. Складіть назви сполук...
2 - Подберите слова паронимы ....
3 - Подбери к каждому слову подственую больше слов с приставками запиши....
2 - Переведите текст и ответьте на вопросы...
1 - Из какого вещества сделан шарик массой 25г, если для его нагревания...
3 - решить эти два задания по физике....
2 - Help me)229292202202002020223004040403030220020202200...
1
Уравнение касательной к графику функции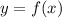 в точке
в точке 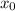 имеет вид:
имеет вид:
1.
Уравнение касательной:
2.
Уравнение касательной: