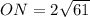Напишите решение и ответтема четыре замечательные точки треугольники

Question

Алгебра: Напишите решение и ответтема четыре замечательные точки треугольники

dddddkkke · Answer

MK и EF - медианы, а все три медианы пересекаются в одной точке. Поэтому если продолжить NO до пересечения с ME в точке L, отрезок NL будет третьей медианой. Как известно, медианы в точке пересечения делятся в отношении 2:1, считая от вершины. Поэтому MO=10; EO=12; OL - треть NL. Продолжим OL за точку L на отрезок OL; получаем точку A и четырехугольник MAEO, который является параллелограммом по признаку параллелограмма (диагонали в точке пересечения делятся пополам). Более того, он является прямоугольником, поскольку угол MOE прямой. В прямоугольнике диагонали равны, то есть AO=ME. А нужный нам отрезок ON равен AO. Остается применить теорему Пифагора:

$ON^2=AO^2=ME^2=MO^2+EO^2=10^2+12^2=2^2(5^2+6^2)=2^2\cdot 61.$