1. Алгебра
  2. Написать уравнение касательной

Написать уравнение касательной в точке х0=3 к графику функции у=(х-1)^3

КристиGirl КристиGirl    3   20.07.2019 17:30    0

Ответы
АмерикаСингер852 АмерикаСингер852  03.10.2020 09:05
Т.к. значение х0 отсутствует в условии, решу в общем виде (в итоговую формулу можно будет подставлять любые значения х0).

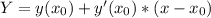
Y=y(x_{0})+y'(x_{0})*(x-x_{0})

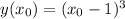
y(x_{0})=(x_{0}-1)^{3}
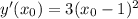
y'(x_{0})=3(x_{0}-1)^{2}

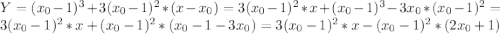
Y=(x_{0}-1)^{3}+3(x_{0}-1)^{2}*(x-x_{0})=3(x_{0}-1)^{2}*x+(x_{0}-1)^{3}-3x_{0}*(x_{0}-1)^{2}=3(x_{0}-1)^{2}*x+(x_{0}-1)^{2}*(x_{0}-1-3x_{0})=3(x_{0}-1)^{2}*x-(x_{0}-1)^{2}*(2x_{0}+1)
ПОКАЗАТЬ ОТВЕТЫ
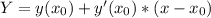
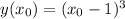
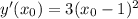
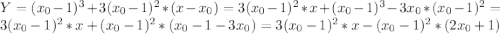
Другие вопросы по теме Алгебра
mollayevadinara mollayevadinara  01.04.2019 15:10
Напишити подробное решение 84/5log5^7...
vovamandrik060p09ui1 vovamandrik060p09ui1  01.04.2019 15:10
Сухая цементная смесь состоит из цемента и песка ,взятых в отношении 1: 3. сколько килограммов цемента необходимо взять, чтобы получить 2 тонна цементной смеси?...
Olga2907 Olga2907  01.04.2019 15:10
Запишите пропорцию ,крайние члены которой равны 128 и 2,а один из средних членов равен 64.найдите неизвестный средний член составленной пропорции...
NovaHelper NovaHelper  01.04.2019 15:10
7розв язати рівняння: а) (8х+3)²-6(3х-1)(3х+1)-5(2х+1)(х-4)=3 б) (3х+1)²-100=0...
Василина914 Василина914  01.04.2019 15:10
1.поезд за 2ч 30 минут проехал расстояние,меньше 200 км.оцените скорость движения поезда. 2.периметр квадрата больше 16 см,но меньше 20 см.оцените длину стороны квадрата....
  24.05.2019 23:50
1)найдите значение выражения: 0,6 (-2)^3+ 0,4 (-2)^2+3=0...
LJкрасотка2007 LJкрасотка2007  24.05.2019 23:50
Уруслана в бутылке было фанты на 10%больше ,чем у никиты . руслан отпил из своей бутылки 11% ее содержимого , а никита из своей -2% содержимого. у кого после этого...
ВладВишня ВладВишня  24.05.2019 23:50
. артемотвечаетзачасна15вопросов, а миша - на 18. они одновременно начали отвечать на вопросытеста, и артем закончил свой тест позже миши на 56 минут. сколько вопросов...
Grundyy Grundyy  24.05.2019 23:50
Найдите значение a при котором равны значения выражений 15а + 8 и 17а - 12...
FedShar28 FedShar28  24.05.2019 23:50
Дописать к цифры так,что бы полученное шестизначное число делилось на 7,8 и 9....

Популярные вопросы