Надо перевести в sin,cos,tg,ctg 1.720°
2.225°
3.300°
4.870°
5.900°
6.-330°
7.-630°
8.-210°
9.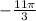
10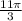
Другие вопросы по теме Алгебра
Популярные вопросы
- Как Мюнхаузен попал к себе в дом, если верить его рассказам?...
1 - Сабақтың тақырыбы: Тұздар (1)(172-176 беттер)1. Орта тұздар қатарын...
2 - Use the hints and the pictures to do the crossword....
2 - Прочитайте текст и выполните задания В1-В3 (1)Как известно, выразительность...
3 - Плл тест по кпзахскомк токо плл правильно ответте 1) Түбір сөзді...
3 - Дана блок начало ввод a,b R:3b M:= 2a P: = R+ M вывод P конец...
2 - сделать! Кроссворд на тему: Лёгкая атлетика . Кроссворд должен...
2 - Задание. Характерные особенности правил в рубриках языковых ориентиров,...
3 - какой отдел мозга пресимкающегосяЦентр регуляции пищеварения:А.промежуточныйБ.мозжечокВ.средний...
3 - Про criket на английском языке...
2
Основные углы, чьи значения мы обычно запоминаем:
- 0°: sin(0°) = 0, cos(0°) = 1, tg(0°) = 0, ctg(0°) - не определено
- 30°: sin(30°) = 1/2, cos(30°) = √3/2, tg(30°) = 1/√3, ctg(30°) = √3
- 45°: sin(45°) = √2/2, cos(45°) = √2/2, tg(45°) = 1, ctg(45°) = 1
- 60°: sin(60°) = √3/2, cos(60°) = 1/2, tg(60°) = √3, ctg(60°) = 1/√3
- 90°: sin(90°) = 1, cos(90°) = 0, tg(90°) - не определено, ctg(90°) = 0
Теперь рассмотрим каждый из предложенных углов и найдём их значения sin, cos, tg и ctg:
1. 1.720°:
Мы не знаем значение sin, cos, tg и ctg для угла 1.720°, но можем написать его в виде суммы 1° и 0.720°.
1° очень близко к 30°, а 0.720° близко к 45°, поэтому мы можем использовать приближенные значения для sin, cos, tg и ctg, равные: sin(1°) ≈ sin(30°) = 1/2, cos(1°) ≈ cos(30°) = √3/2, tg(0.72°) ≈ tg(45°) = 1, ctg(0.72°) ≈ ctg(45°) = 1.
Таким образом, для угла 1.720° получаем:
sin(1.720°) ≈ sin(1°) = 1/2
cos(1.720°) ≈ cos(1°) = √3/2
tg(1.720°) ≈ tg(0.720°) ≈ tg(45°) = 1
ctg(1.720°) ≈ ctg(0.720°) ≈ ctg(45°) = 1.
2. 2.225°:
Мы видим, что данный угол близок к 30°, поэтому мы можем использовать приближенные значения синуса, косинуса, тангенса и котангенса, равные: sin(2.225°) ≈ sin(30°) = 1/2, cos(2.225°) ≈ cos(30°) = √3/2, tg(2.225°) ≈ tg(30°) = 1/√3, ctg(2.225°) ≈ ctg(30°) = √3.
3. 3.300°:
Мы видим, что данный угол близок к 60°, поэтому мы можем использовать приближенные значения синуса, косинуса, тангенса и котангенса, равные: sin(3.300°) ≈ sin(60°) = √3/2, cos(3.300°) ≈ cos(60°) = 1/2, tg(3.300°) ≈ tg(60°) = √3, ctg(3.300°) ≈ ctg(60°) = 1/√3.
4. 4.870°:
Мы видим, что данный угол близок к 60°, поэтому мы можем использовать приближенные значения синуса, косинуса, тангенса и котангенса, равные: sin(4.870°) ≈ sin(60°) = √3/2, cos(4.870°) ≈ cos(60°) = 1/2, tg(4.870°) ≈ tg(60°) = √3, ctg(4.870°) ≈ ctg(60°) = 1/√3.
5. 5.900°:
Мы видим, что данный угол близок к 90°, поэтому мы можем использовать приближенные значения синуса, косинуса, тангенса и котангенса, равные: sin(5.900°) ≈ sin(90°) = 1, cos(5.900°) ≈ cos(90°) = 0, tg(5.900°) - не определено, ctg(5.900°) = ctg(90°) = 0.
6. -330°:
Угол -330° можно представить в виде суммы -360° и 30°.
-360° соответствует 0°, а 30° соответствует значению sin, cos, tg и ctg из пункта 2.
7. -630°:
Угол -630° можно представить в виде суммы -720° и 30°.
-720° соответствует 0°, а 30° соответствует значению sin, cos, tg и ctg из пункта 2.
8. -210°:
Угол -210° можно представить в виде суммы -180° и -30°.
-180° соответствует 0°, а -30° соответствует значению sin, cos, tg и ctg из пункта 2.
9. -11π/3:
Для перевода угла из радиан в градусы, мы должны знать, что 180° соответствует π радианам.
Таким образом, угол -11π/3 равен (-11π/3) * (180°/π) = -660°.
Мы видим, что данный угол близок к -630°, поэтому мы можем использовать приближенные значения синуса, косинуса, тангенса и котангенса, равные: sin(-11π/3) ≈ sin(-630°) = sin(30°) = 1/2, cos(-11π/3) ≈ cos(-630°) = cos(30°) = √3/2, tg(-11π/3) ≈ tg(-630°) = tg(30°) = 1/√3, ctg(-11π/3) ≈ ctg(-630°) = ctg(30°) = √3.
10. 11π/3:
Аналогично, угол 11π/3 равен (11π/3) * (180°/π) = 660°.
Мы видим, что данный угол близок к 630°, поэтому мы можем использовать приближенные значения синуса, косинуса, тангенса и котангенса, равные: sin(11π/3) ≈ sin(630°) = sin(30°) = 1/2, cos(11π/3) ≈ cos(630°) = cos(30°) = √3/2, tg(11π/3) ≈ tg(630°) = tg(30°) = 1/√3, ctg(11π/3) ≈ ctg(630°) = ctg(30°) = √3.
Таким образом, получаем ответ:
1.720°: sin(1.720°) ≈ 1/2, cos(1.720°) ≈ √3/2, tg(1.720°) ≈ 1, ctg(1.720°) ≈ 1.
2.225°: sin(2.225°) ≈ 1/2, cos(2.225°) ≈ √3/2, tg(2.225°) ≈ 1/√3, ctg(2.225°) ≈ √3.
3.300°: sin(3.300°) ≈ √3/2, cos(3.300°) ≈ 1/2, tg(3.300°) ≈ √3, ctg(3.300°) ≈ 1/√3.
4.870°: sin(4.870°) ≈ √3/2, cos(4.870°) ≈ 1/2, tg(4.870°) ≈ √3, ctg(4.870°) ≈ 1/√3.
5.900°: sin(5.900°) ≈ 1, cos(5.900°) ≈ 0, tg(5.900°) - не определено, ctg(5.900°) ≈ 0.
6.-330°: sin(-330°) ≈ 1/2, cos(-330°) ≈ √3/2, tg(-330°) ≈ 1/√3, ctg(-330°) ≈ √3.
7.-630°: sin(-630°) ≈ 1/2, cos(-630°) ≈ √3/2, tg(-630°) ≈ 1/√3, ctg(-630°) ≈ √3.
8.-210°: sin(-210°) ≈ 1/2, cos(-210°) ≈ √3/2, tg(-210°) ≈ 1/√3, ctg(-210°) ≈ √3.
9.-11π/3: sin(-11π/3) ≈ 1/2, cos(-11π/3) ≈ √3/2, tg(-11π/3) ≈ 1/√3, ctg(-11π/3) ≈ √3.
10.11π/3: sin(11π/3) ≈ 1/2, cos(11π/3) ≈ √3/2, tg(11π/3) ≈ 1/√3, ctg(11π/3) ≈ √3.
Приближенные значения синуса, косинуса, тангенса и котангенса, которые были использованы в решении задачи, являются приближениями и могут отличаться от точных значений.