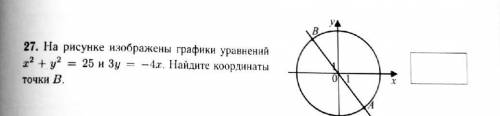
На рисунке изображены графики уравнений x^2+y^2=25 3y=-4x Найдите координаты точки B
Другие вопросы по теме Алгебра
Популярные вопросы
- Сумма четырёх натуральных чисел равна 348. три числа являются последовательными...
2 - Цирк - вид искусства, объединяющий выступления акробатов, гимнастов, клоунов, эквилибристов,...
2 - Чему равна степень окисления элементов в соединениях: a)na2b4o7; б)bi2(so4)3? определите...
3 - Почему к эпитету коза-дереза толкование в словаре даля беляк,ракитник,чапыжник?...
2 - Самолет заходит на посадку со скоростью 200 км ч и до полоной остановки пробегает...
3 - На сторонах угла вас,равного 20,и на его биссектрисе отложены равные отрезки ав,ас...
2 - (1878+9567-6413): 68 как правильно решать в столбик?...
1 - 27. translate these sentences into english. using modals or their equivalents. a....
1 - Составить электронную формулу атома 14si...
2 - Длина сухопутной границы россии с китаем,монголии казахстаном составляет 15293 км....
1
В точке B графики пересекаются, значит, их ординаты равны.
Произведение равно нулю, когда хотя бы один из множителей равен нулю.
Оба корня подходят, но на графике видно, что у точки B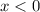 , поэтому её абсцисса
, поэтому её абсцисса 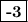 . Найти ординату мы можем, подставив данную абсциссу в любое уравнение.
. Найти ординату мы можем, подставив данную абсциссу в любое уравнение.
Таким образом, координаты точки B: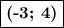 .
.