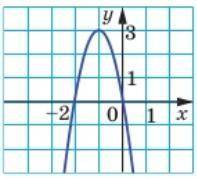
На рисунке изображен график функции y = -3x²-6x. Найдите множество решений неравенства:

Для решения неравенства, нам нужно определить интервалы на графике функции, на которых значение y больше или меньше нуля.

Заметим, что график функции y = -3x²-6x является параболой, которая открывается вниз.

1. Найдём вершину параболы, используя формулу x = -b/2a, где a и b - коэффициенты квадратичного уравнения.
В нашем случае, a = -3, b = -6, поэтому x = -(-6)/(2*(-3)) = 1.
Таким образом, вершина параболы имеет координаты (1, f(1)), где f(1) - значение функции в точке x = 1.

2. Определим, где парабола находится относительно оси x.
Если a < 0, парабола открывается вниз и все значения y будут меньше нуля.
Если a > 0, парабола открывается вверх и все значения y будут больше нуля.
В нашем случае, a = -3, поэтому парабола открывается вниз и все значения y будут меньше нуля.

3. Теперь рассмотрим, какие значения y функции находятся выше и ниже оси x.
Заметим, что вершина параболы находится выше оси x, поэтому все значения y ниже оси x будут меньше нуля.

Итак, множество решений неравенства выглядит следующим образом: y < 0.

Пояснение: Все точки на графике функции, которые находятся ниже оси x, будут иметь значения y меньше нуля. Поэтому, для любого x на графике, значение функции y = -3x²-6x будет меньше нуля.

Надеюсь, мой обстоятельный ответ помог вам понять решение этой задачи! Если у вас возникнут ещё вопросы, не стесняйтесь задавать!