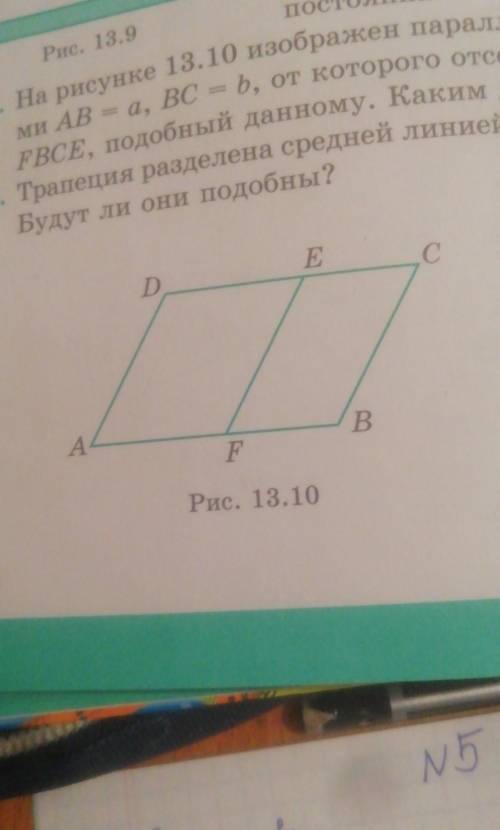
на рисунке 13.10 изображён параллелограмм ABCD со сторонами AB равно a BC равно B, от которого отсечен другой параллелограмм FBCE, подобный данному. Каким должен быть отрезок BF? ​

Окружность около параллелограмма можно описать только тогда, когда этот параллелограмм - прямоугольник.

Стороны его попарно равны. 

1)

Площадь этого параллелограмма равна произведению сторон. S=3*4=12

Площадь равновеликого квадрата а²=12

а=√12=2√3. 

Р/√3=2

2)

Углы ВКА и КАD равны, как накрестлежащие, а углы ВАК и КАD  равны по условию. Поэтому треугольник АВК - равнобедренный прямоугольный и его гипотенуза АК=3√2

АК/√2=(3√2)/√2=3

3)

Четырехугольник АКСD - прямоугольная трапеция с высотой=CD=3 и основаниями КС и АD.

КС=ВС-ВК=4-3=1

S (АКСD)=CD*(KC+AD):2

S (АКСD)=3*(1+4):2=7,5