на решение задачу срошно надо ???)
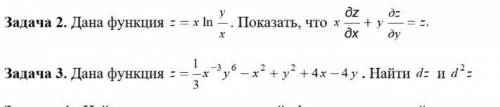
Другие вопросы по теме Алгебра
Популярные вопросы
- Перечислите основные при птиц к полёту...
2 - .(Найдите три последовательных числа, если произведение двух меньших чисел меньше...
3 - Нагреватель из нихромовой проволоки длиной 5 м и диаметром 0,25 мм включается в...
2 - .(Усвиней черная окраска щетины доминирует над рыжей, а длинная щетина -над короткой....
2 - Вычисли массовую долю аммиака в растворе полученном при растворении 700 мл nh3...
3 - Каков общий характер поверхности южной америки...
1 - .(Вычислите объём водорода (н. у.) , который образутся при растворении 7,2 магния...
1 - Втрапеции abcd даны основания ad=8, bc=4. на продолжении bc выбрана точка м такая,...
2 - Настоящее и будущее время глаголов...
3 - .(Что называют слова сырой, мокрый. всегда ли слово сырой означает мокрый? придумай...
1
2
Подставим в равенство:
равенство выполняется
3
_____________