Моторная лодка по течению реки 27 км за время, которое ей потребуется, чтобы пройти 21 км против течения . найти скорость течения реки, если собственная скорость лодки 8 км/ч. нудно записать в виде и решить завтра гос.экзамен

Ответы

бооой 03.07.2020 13:26

1 км/ч

Объяснение:

Пусть x - скорость течения реки. Тогда 8+x - скорость по течению, 8-x - скорость против течения,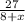 $\frac{27}{8+x}$ - время, за которое она км по течению, а 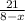$\frac{21}{8-x}$ - время, за которое она км против течения. По условию эти времена равны. Составим и решим уравнение:

$\frac{27}{8+x}$ = $\frac{21}{8-x}$

Перенесём правую дробь в левую часть уравнения:

$\frac{27}{8+x}$ - $\frac{21}{8-x}$ =0

Приведём к общему знаменателю:

$\frac{(27*(8-x))-(21*(8+x))}{(8-x)*(8+x)}$ =0

$\frac{216-27x-168-21x}{64-x^{2} }$ =0

$\frac{48-48x}{64-x^{2} }$ =0

Знаменатель не должен быть равен 0, т.е. x≠±8

А числитель приравниваем к 0:

48-48x=0

48x=48

x=1

Т.е. скорость течения реки=1 км/ч

ПОКАЗАТЬ ОТВЕТЫ

shutilkaha 03.07.2020 13:26

1 км\час.

Объяснение:

Пусть скорость течения реки х км\час, тогда скорость лодки по течению х+8 км\час, скорость против течения 8-х км\час. Составим уравнение по условию задачи:

27\(х+8) = 21\(8-х)

216-27х=168+21х

48х=48

х=1.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра