мне 2.189. При каких значениях переменной x:
1) сумма дробей
6/x+1 и x/x-2;
2) разность дробей
x+12/x-4 и x/x+4 равна их произведению?
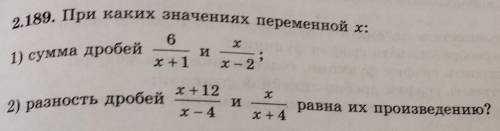
Другие вопросы по теме Алгебра
Популярные вопросы
- Палисад имеет форму прямоугольника, стороны которого равны 2,5 м и 7 м. длинной...
2 - Найдите причастный и деепричастный .вот сам .текст: жил на свете мальчик лёня....
3 - Стальное колечко сказка или рассказ...
1 - Что понимается под правовыми отношениями? какими отраслями права они регулируются?...
1 - Найти ошибки связанные с неправильным словообразованием: некоторые приехали...
1 - Найдите натуральные значения b , при которых данное неравенство равно...
1 - Почему волка называют санитаром леса?...
3 - Вычислите наиболее удобным...
2 - Указать падеж прилагательных отряд туристов забрел в лесную глушь...
3 - Убібліотеці класу є 48 книжок з оповіданнями це 2/7 усієї кількості книжок....
1
1) Найдем сумму данных дробей:
6/(x+1) + x/(x-2)
Для сложения дробей с разными знаменателями, нам нужно найти общий знаменатель. В данном случае, общим знаменателем будет (x+1)*(x-2).
Теперь приведем каждую дробь к общему знаменателю:
6*(x-2)/[(x+1)*(x-2)] + x*(x+1)/[(x+1)*(x-2)]
Складываем числители и оставляем общий знаменатель:
(6*(x-2) + x*(x+1))/[(x+1)*(x-2)]
Упрощаем числитель:
(6x - 12 + x^2 + x)/[(x+1)*(x-2)]
Собираем все вместе:
(x^2 + 7x - 12)/[(x+1)*(x-2)]
2) Найдем разность данных дробей:
(x+12)/(x-4) - x/(x+4)
Приведем каждую дробь к общему знаменателю, который в данном случае будет (x-4)*(x+4):
(x+12)*(x+4)/[(x-4)*(x+4)] - x*(x-4)/[(x-4)*(x+4)]
Складываем числители и оставляем общий знаменатель:
[(x+12)*(x+4) - x*(x-4)]/[(x-4)*(x+4)]
Упрощаем числитель:
(x^2 + 16x + 48 - x^2 + 4x)/[(x-4)*(x+4)]
Собираем все вместе:
(20x + 48)/[(x-4)*(x+4)]
Теперь поставим условие, что сумма и разность дробей должны быть равны их произведению:
(x^2 + 7x - 12)/[(x+1)*(x-2)] = (20x + 48)/[(x-4)*(x+4)]
Умножаем обе стороны уравнения на [(x+1)*(x-2)] * [(x-4)*(x+4)] (комплексный знаменатель обеих дробей):
(x^2 + 7x - 12) * [(x-4)*(x+4)] = (20x + 48) * [(x+1)*(x-2)]
Раскрываем скобки:
(x^2 + 7x - 12) * [(x^2-16)*(x^2-3)] = (20x + 48) * [(x^2-1)*(x^2-4)]
Упрощаем уравнение и приводим его к квадратному виду:
(x^2 + 7x - 12) * (x^4 - 19x^2 + 48) = (20x + 48) * (x^4 - 5x^2 + 4)
Раскрываем скобки:
x^6 - 19x^4 + 48x^2 + 7x^3 - 133x - 336 = 20x^5 - 100x^3 + 80x + 192
Приводим подобные члены:
x^6 - 20x^5 + 19x^4 + 107x^3 - 133x - 416 = 0
Это кубическое уравнение, которое является сложным для решения аналитически. Оно может быть решено численными или графическими методами.
Вывод: для решения данного кубического уравнения и определения значений переменной x, при которых сумма и разность данных дробей будет равна их произведению, необходимо использовать численные или графические методы.