Найти общее решение: 2y'=y^2/x^2+6*y/x+3
Другие вопросы по теме Алгебра
Популярные вопросы
- Напишите план к сказке мальчик-с-пальчик,если что нужно 5 частей,заранее...
2 - Короткий рассказ на тему: если был бы я дениской ( денискины рассказы)...
1 - Врезультате какого из произведений векторов будет получатся число? варианты...
2 - Не могу понять как сделать деление используя запись уголком....
1 - Выписать слова с безударными гласными и парными согласными и подобрать...
3 - Выражение синус альфа в квадрате + косинус альфа в квадрате +тангенс...
1 - Дополни условие, составь по выражение и реши их. катя купила 2 одинаковые...
1 - На одной чашке весов лежат 12 апельсинов, а на другой 4 дыни . если...
1 - Найти номер n-го члена арифметической прогрессии, если а)an=60, а2=11,...
1 - Подберите и запишите аноним к слову утрений...
1
Это дифференциальное уравнение является однородным. Воспользуемся заменой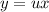 , тогда дифференцируя обе части, имеем
, тогда дифференцируя обе части, имеем 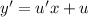 . Подставляем в исходное уравнение
. Подставляем в исходное уравнение
Получили уравнение с разделяющимися переменными
Сделаем обратную замену: u = y/x, получим
Получили общий интеграл.