1. Алгебра
  2. Mатематический индукция

Mатематический индукция 1*3+2*5++n(2n+1)=n(n+1)(4n+5)/6 нужно доказать . !

Коля12Коля Коля12Коля    1   11.09.2019 21:52    2

Ответы
StasuxaStasyan StasuxaStasyan  07.10.2020 08:20

В равенстве слева сумма имеет общий член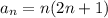 a_n=n(2n+1)

1) Базис индукции: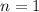 n=1

1\cdot (2\cdot 1+1)=\dfrac{1\cdot (1+1)\cdot (4\cdot 1+5)}{6}~~~\Rightarrow~~~ 3=3

2) Предположим, что и для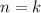 n=k верно равенство

1\cdot 3+2\cdot 5+...+k(2k+1)=\dfrac{k(k+1)(4k+5)}{6}

3) Индукционный переход: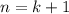 n=k+1

\underbrace{1\cdot 3+2\cdot 5+...+k(2k+1)}_{\frac{k(k+1)(4k+5)}{6}}+(k+1)(2k+3)=\dfrac{(k+1)(k+2)(4k+9)}{6}\\ \\\\\dfrac{k(k+1)(4k+5)}{6}+(k+1)(2k+3)=\dfrac{(k+1)(k+2)(4k+9)}{6}\\ \\ \\ (k+1)\left(\dfrac{k(4k+5)}{6}+2k+3\right)=\dfrac{(k+1)(k+2)(4k+9)}{6}\\ \\ \\ (k+1)\cdot \dfrac{4k^2+5k+12k+18}{6}=\dfrac{(k+1)(k+2)(4k+9)}{6}\\ \\ \\ \dfrac{(k+1)(4k^2+17k+18)}{6}=\dfrac{(k+1)(k+2)(4k+9)}{6}\\ \\ \\ \dfrac{(k+1)(k+2)(4k+9)}{6}=\dfrac{(k+1)(k+2)(4k+9)}{6}

Равенство выполняется для всех натуральных n. Что и требовалось доказать.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
cat73309owz9do cat73309owz9do  15.05.2020 10:53
О чём говорится в сказке про маленького робота...
Meow444 Meow444  15.05.2020 10:53
Тут смешана геометрия и алгебра. ОТВЕТЫ С РЕШЕНИЕМ, ЕСЛИ ИХ НЕ БУДЕТ, ТО Я БУДУ ВЫНУЖДЕНА КИНУТЬ НАРУШЕНИЕ...
gumballl1 gumballl1  15.05.2020 10:53
Выполните умножение многочленов: (3а-в)(2в+4а) 1)12а2(степень)-2ав-2в2(степень); 2)12а2(степень)+2ав-2в2(степень); 3)6ав-2в2(степень); 4)6ав-4в....
Starostina2018 Starostina2018  11.05.2020 11:19
Используя теорему Виета составьте квадратное уравнение по его корням 1 и 2/3...
диана2460 диана2460  11.05.2020 11:19
Найдите общий вид первообразных для функций...
denian11343 denian11343  11.05.2020 11:25
Пять землекопов за 5 часов выкапывают 5 м канавы. Сколько потребуется землекопов, для того чтобы выкопать 100 м канавы за 100 часов...
френки9 френки9  11.05.2020 11:24
Являются ли возможным и невозможными события, состоящие в том,что при однократном бросании кости выпадет 5 очков, 7 очков, от 1 до 6 очков? Какие события в этом испытании...
kek200570 kek200570  11.05.2020 11:24
Построить график функции y=4^x и опишите основные свойства функции....
klybnika228 klybnika228  11.05.2020 11:24
1. [ ] При каких значениях переменной х, алгебраическая дробь4x 2 -2x -3/(x-3)(x+3) имеет смысл?...
198206nh 198206nh  11.05.2020 11:23
1. Из пункта А в пункт Б выехал велосипедист, а через 3/2 часа за ним выехал автомобилист. Оба двигались с постоянными скоростями. На 1/2 пути из А в Б автомобилист догнал...

Популярные вопросы