1. Алгебра
  2. Logx^2(3-2x) 1 решите логарифмическое

Logx^2(3-2x)>1 решите логарифмическое неравенство

oxpoluhina2017 oxpoluhina2017    2   10.06.2020 11:00    11

Ответы
HeavenSent HeavenSent  15.10.2020 13:35

Введем ограничения:

\displaystyle \left \{ {{3-2x0} \atop {x^20; x^2\neq 1}} \right.\\\\\left \{ {{x

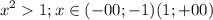
1 случай \displaystyle x^21; x \in (-00;-1) (1;+00)

тогда логарифм - возрастающая функция

\displaystyle 3-2xx^2\\\\x^2+2x-3

с учетом условия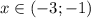 \displaystyle x \in (-3;-1)

2 случай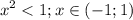 \displaystyle x^2

логарифм убывающая функция

\displaystyle 3-2x0\\\\ x \in (-oo;-3) (1; +oo)

с учетом условия : решений нет

Окончательный ответ  (с учетом ограничений) (-3;-1)

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Vadim12045683777779 Vadim12045683777779  13.05.2020 14:34
9 класс задача, обязательно с объяснением​...
zaharkakorsunov zaharkakorsunov  13.05.2020 14:33
Дано квадратное уравнение x2−8,7x−2,8=0, укажи сумму и произведение корней...
olesasumakova8ozf25j olesasumakova8ozf25j  13.05.2020 14:33
1. Розв яжіть систему рівнянь 4х+у2=-8 х2-у2=4 2. У двох ящиках лежать яблука якщо з одного перекласти до другого 45 яблук то в обох ящиках стане яблук порівну....
pollvasiltv pollvasiltv  13.05.2020 14:33
Расстояние между двумя населёнными пунктами по реке равно 140 км. Это расстояние катер проплывает по течению реки за 5 ч., а против течения — за 7 ч. Найди собственную...
zolotuk123 zolotuk123  13.05.2020 14:33
Яке число є сумою коренів квадратного рівняння х2 – 3х – 18 = 0?​...
missmekhtiyeva110803 missmekhtiyeva110803  13.05.2020 14:33
Разложите на множители. Один пример. Большего не...
AiDanttlll AiDanttlll  13.05.2020 14:33
Швидкисть катера за тичиею рички доривнюе 21км/год, а проти - 15км/год. Знайдить власну швидкисть катера....
gdrsfdfsfss gdrsfdfsfss  13.05.2020 14:33
При якому значенні a система рівнянь 7x-4y = 3 має безліч розв язків ax- 8y = 6 ax-8y = 6...
shapuk shapuk  14.05.2020 11:13
В приложении во на фото. Вычислите интеграл: ∫1x6dx -1...
Meryem98 Meryem98  14.05.2020 11:13
Знайдiть координати середини вiдрiзка АВ, якщо А(-2;4), В(8;-12)....

Популярные вопросы