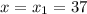Log5 (3x-11)+log5 (x-27)=3+log5 8 решите нада.
Другие вопросы по теме Алгебра
Популярные вопросы
- Какое настроение удалось создать левигтону золотая осень...
1 - Написать описание индийского океана , согласно плану учебника...
1 - 100 цукерок знаходяться у 50 коробках. дівчинка і хлопчик по черзі...
1 - Назовите глаголы, от которых образованы следующие существительные:...
1 - Найти в толковом словаре два фразеологизма и составить предложение...
3 - Все дачники были приглашены к утреннему чаю разабрать по составу...
1 - Акшаны сактау накты сози калай болады...
1 - Скорость обращения луны вокруг солнца 3600км/ч что составляет...
1 - Вычислите ((32/р)^2/5 *р^1/5)/(р^-3)...
1 - Длина прыжка льва 15м а длина прыжка антилопы на 1/3 меньше длины...
1
ОДЗ нашего уравнение:
Преобразуем левую часть уравнения, используя тождество:
В нашем случае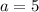 ,
, 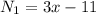 ,
, 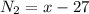
Поэтому![log_{5}(3x-11)+log_{5}(x-27)=log_{5}[(3x-11)(x-27)]](/tpl/images/0043/5175/0c853.png) ------(2)
------(2)
Правую часть нашего уравнения также преобразуем с тождества (1), предварительно представив слагаемое 3 в виде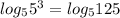 :
:
C учетом (2) и (3) исходное уравнение примет вид:
Отсюда по свойству логарифма получим алгебраическое уравнение:
Найдем его дискриминант: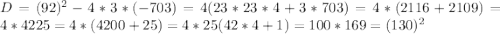
Поскольку дискриминант положителен, то квадратное уравнение имеет два различных действительных корня:
Таким образом, только один корень квадратного уравнения является корнем исходного уравнения: