Log₃(x+1)+log₃(x+3)> 1 заранее больше
Другие вопросы по теме Алгебра
Популярные вопросы
- Хімічні властивості 2,3-диметил бутан...
1 - Докажите, что при всех значениях параметра а расстояние между...
3 - 1. помимо различий, чем отличаются мужчины и женщины? 2. как...
2 - составьте с любой парой омонимов два предложения. подчеркните...
1 - Преобразуйте произведение в многочлен: 4) (-1/3b)•(-9b²+3b-12);...
3 - Коли пасажири увійшли в порожній трамвай, 2/7 іх зайняли місця...
1 - Сочинение рассуждение на тему: почему ольге не удалось изменить...
2 - Правописание приставок 1. в каком слове правописание приставки...
2 - Выращивание кристаллов из медного купороса. можно ли заливать...
1 - Как в рассказе тупейный художник отмечается крепостное право?...
1
Запишем ОДЗ: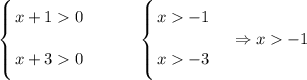
Упростим неравенство:
Объединим неравенство с ОДЗ:
ответ: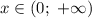
* Решение данного неравенства упущено (оно решается методом интервалов или парабол).