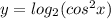Log^2 (2) (cos^2x)-22log2(cosx)-12=0 решить
Другие вопросы по теме Алгебра
Популярные вопросы
- Меня зовут ульяна мне двинадцать лет...
3 - Написать информацию про опасную профессию ...
2 - [tex]6215 \div 5 \\ 7860 \div 5 \\ 4590\div 5 \\ 9485 \div 5 \\...
3 - 558. измерь дома диаметры и длины окружностей двух различных стаканов...
3 - Перевести в косвенную речь, 50б! ...
3 - составить рассказ на языке не про учёного ...
3 - Напишыте письмо танап это сказка три желания на грамотаны канешно...
3 - Нужна завтра самостоятельна...
2 - Слогарифмами, заранее огромное !...
3 - Составить на тему линейное уравнение с одной переменной...
3
ОДЗ : cos x > 0
Замена переменной