Limx стремится к нулю ln(1+3x^2)/x^3-5x^2
Другие вопросы по теме Алгебра
Популярные вопросы
- Прочитай поговорки. Мороз невелик, да стоять не велит. На морозе...
1 - Спиши. Найди слова, которые одинаково пишутся. Поставь знак...
3 - Прочитай. На жарком солнышке подсох и рвётся из стручков горох....
3 - Прочитай пословицы. Дело мастера боится. Без работы день годом...
1 - Прочитай. Какое слово пропущено? Жеребёнок Хвост — косичкой,...
3 - Прочитай. Шли ребята по улице, а по дороге ехали: блестящий...
1 - Спиши, разделяя слова знаком переноса. Киоск, театр, крикнул,...
3 - Спиши, разделяя слова знаком переноса. Удар, линия, радио, здание,...
1 - Измени данные слова по образцу. Напиши. Рисуют — рисуйте, играют...
3 - Составь из данных слов предложения. Какой знак ты поставишь...
3
Воспользуемся эквивалентностью функции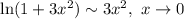
ответ и решение во вложении