Контрольная работа по Алгебре

номер 1
Постройте график линейной функции у=2х-3. С графика найдите:
а) значение у , если х=3
б) значение х , если у= -1
в) значение переменной х, при которых значения функции отрицательные.

номер 2
Найдите координаты точки пересечения прямых
у=-х и у=х-8.

номер 3
а) Найдите координаты точки пересечения графика линейной функции у=-2х+6 с осями координат .
б) определите принадлежит ли графику данной функции точка М(15; -24)

номер 4
В одной и той же системе координат постройте график функции : а) у=2х б) у=4

номер 5
Задайте линейную функцию у=кх формулой , если известно, что ее график параллелен прямой у=-4х+7.

номер 6
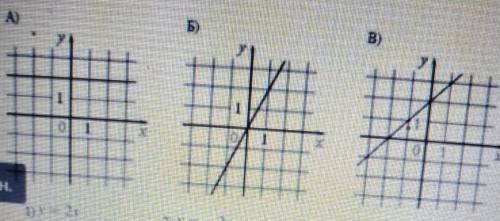
установите соответствие между графиками функции и формулами , которые их задают.
(( на фото номер 6 )))
1)у = 2х 2)у=-2х 3) у=х+2
4) y=2 .
​

Номер 1:
а) Чтобы найти значение у, когда х=3, мы подставляем х=3 в уравнение функции у=2х-3:
у=2х-3
у=2(3)-3
у=6-3
у=3

Ответ: значение y равно 3, когда х=3.

б) Чтобы найти значение х, когда у=-1, мы подставляем у=-1 в уравнение функции у=2х-3:
-1=2х-3
Добавляем 3 ко всем членам уравнения:
-1+3=2х-3+3
2=2х
Разделяем обе части уравнения на 2:
х=1

Ответ: значение x равно 1, когда у=-1.

в) Чтобы найти значение переменной х, при котором значения функции отрицательные, мы должны рассмотреть, когда у<0:
у=2х-3
2х-3<0
Добавляем 3 ко всем членам уравнения:
2х<3
Разделяем обе части уравнения на 2:
х<3/2

Ответ: значения х будут отрицательными, когда х<3/2.

Номер 2:
Чтобы найти координаты точки пересечения прямых у=-х и у=х-8, мы должны решить следующую систему уравнений:
у=-х
у=х-8

Подставляем у=-х во второе уравнение:
-х=х-8
Добавляем х к обеим сторонам уравнения:
0=2х-8
Добавляем 8 к обеим сторонам уравнения:
8=2х
Разделяем обе стороны уравнения на 2:
4=х

Теперь, чтобы найти значение у, мы подставляем х=4 в любое из уравнений:
у=-4

Ответ: координаты точки пересечения прямых равны (4, -4).

Номер 3:
а) Чтобы найти координаты точки пересечения графика линейной функции у=-2х+6 с осями координат, мы должны найти точки, где прямая пересекает оси x и у.

Пересечение с осью x:
у=-2х+6
0=-2х+6
Добавляем 2х к обеим сторонам уравнения:
2х=6
Разделяем обе стороны уравнения на 2:
х=3

Пересечение с осью у:
у=-2х+6
у=-2(0)+6
у=6

Ответ: координаты точки пересечения с осями координат равны (3, 0) и (0, 6).

б) Чтобы определить, принадлежит ли графику данной функции точка М(15, -24), мы должны подставить значения координат точки в уравнение функции и проверить, выполняется ли равенство:
у=-2х+6
-24=-2(15)+6
-24=-30+6
-24=-24

Ответ: точка М(15, -24) принадлежит графику данной функции.

Номер 4:
а) Чтобы построить график функции у=2х, мы должны выбрать несколько значений для х и подставить их в уравнение функции, чтобы найти соответствующие значения у. Затем мы строим точки (х, у) на графике и соединяем их линией.

Выберем несколько значений х:
х=-2, у=2(-2)=-4
х=-1, у=2(-1)=-2
х=0, у=2(0)=0
х=1, у=2(1)=2
х=2, у=2(2)=4

Строим точки: (-2, -4), (-1, -2), (0, 0), (1, 2), (2, 4). Соединяем их линией.

б) Чтобы построить график функции у=4, мы используем аналогичный процесс. Так как эта функция имеет постоянное значение у=4 для всех значений х, мы строим горизонтальную линию на графике на уровне у = 4.

Номер 5:
Чтобы задать линейную функцию у=кх, параллельную прямой у=-4х+7, мы замечаем, что параллельные прямые имеют одинаковый угловой коэффициент. Угловой коэффициент прямой у=-4х+7 равен -4.
Значит, угловой коэффициент нашей линейной функции у=кх также будет равен -4.

Ответ: Заданная линейная функция параллельна прямой у=-4х+7 и имеет формулу у=-4х.

Номер 6:
Для установления соответствия между графиками функции и формулами мы должны изучить графики и свойства каждой функции.

1) График функции у=2х представляет собой прямую линию с положительным угловым коэффициентом. Угловой коэффициент равен 2, что означает, что каждый раз при увеличении х на 1, у увеличивается на 2.

2) График функции у=-2х представляет собой прямую линию с отрицательным угловым коэффициентом. Угловой коэффициент равен -2, что означает, что каждый раз при увеличении х на 1, у уменьшается на 2.

3) График функции у=х+2 представляет собой прямую линию с положительным угловым коэффициентом и сдвигом вверх на 2 единицы. Угловой коэффициент равен 1, что означает, что каждый раз при увеличении х на 1, у увеличивается на 1.

4) График функции y=2 представляет собой горизонтальную прямую линию на уровне у=2. Значение у постоянно и не зависит от значения х.

Ответ:
1) Соответствует графику функции у=2х.
2) Соответствует графику функции у=-2х.
3) Соответствует графику функции у=х+2.
4) Соответствует графику функции у=2.