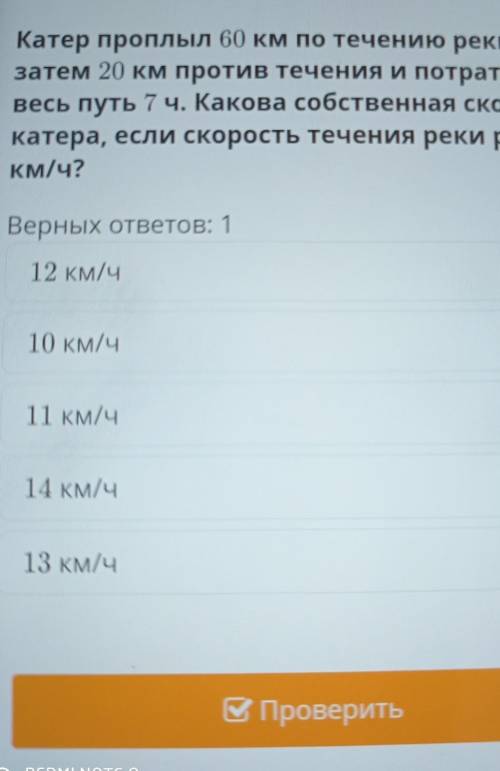
катер проплыл 60 км по течению реки а затем 2 км против течения и потратил на весь путь 7 часов Какова собственная скорость катера если скорость течения реки 1 км ч
Другие вопросы по теме Алгебра
Популярные вопросы
- Загадка у якої відгадка буде композиція...
2 - 2.2. На руинах Западнотюркского каганата тюркские племена образовали ряд госу-...
3 - Периметр катка равен 800 м найдите площадь этого катка если его стороны относятся...
3 - На плоскости даны 5 точек . Через каждую пару этих точек провели прямую. Столько...
1 - «Сегізаяқ» өлеңі стиліндегі олендер қазақ поэзиясында жиі кездесе ме? Хрестоматияда...
1 - Создай синквейн на тему МУЗЫКА...
3 - Запишите методы индефикации физического лица !!...
2 - Периметр прямоугольного треугольника равен 1,8см а его стороны относятся как...
2 - ( ) Составить генетическую связь и ее осуществить (9 класс)...
1 - Назовите пять формул химических элементов...
2
В решении.
Объяснение:
Катер проплыл 60 км по течению реки, а затем 20 км против течения и потратил на весь путь 7 часов. Какова собственная скорость катера, если скорость течения реки 1 км/час?
Формула движения: S=v*t
S - расстояние v - скорость t – время
х - собственная скорость катера.
(х + 1) - скорость катера по течению.
(х - 1) - скорость катера против течения.
60/(х + 1) - время катера по течению.
20/(х - 1) - время катера против течения.
Время в пути 7 часов, уравнение:
60/(х + 1) + 20/(х - 1) = 7
Умножить уравнение на (х + 1)(х - 1), чтобы избавиться от дробного выражения:
60 * (х - 1) + 20 * (х + 1) = 7 * (х + 1)(х - 1)
Раскрыть скобки:
60х - 60 + 20х + 20 = 7х² - 7
Привести подобные члены:
-7х² + 80х - 40 + 7 = 0
-7х² + 80х - 33/-1
7х² - 80х + 33 = 0, квадратное уравнение, ищем корни.
D=b²-4ac = 6400 - 924 = 5476 √D= 74
х₁=(-b-√D)/2a
х₁=(80-74)/14
х₁=6/14
х₁=3/7, отбрасываем, как не отвечающий условию задачи.
х₂=(-b+√D)/2a
х₂=(80+74)/14
х₂=154/14
х₂=11 (км/час) - собственная скорость катера.
Проверка:
60 : 12 = 5 (часов) - по течению.
20 : 10 = 2 (часа) - против течения.
5 + 2 = 7 (часов) - в пути, верно.