Как тригонометрическое уравнение. sin4x+sin5x+sin6x=0
Ответы
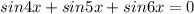
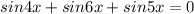
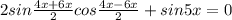
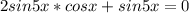
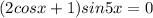
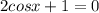 или
или 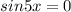
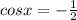 или
или 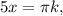
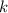 ∈
∈ 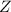
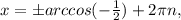
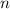 ∈
∈ 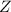 или
или 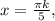
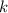 ∈
∈ 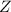
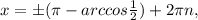
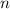 ∈
∈ 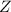
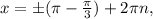
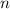 ∈
∈ 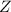
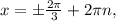
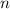 ∈
∈ 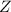
Другие вопросы по теме Алгебра
Популярные вопросы
- Математика 5 класс, на маяке установлены 3 лампы, первая горит 1 раз в 6 сек....
2 - II. Use the right words and word combinations: morming exercises: got up: washed;...
3 - Які гази легші за повітря а які важчі?...
2 - Позначте назву ненасиченої карбонової кислоти: А) стеаринова; Б) олеїнова;...
3 - Світ поліани і уроки доброти 10 речень. іть ...
1 - Read the text and complete the sentences ребята я сам не знаю как это скажитеть...
1 - дама с собачкой.Как изменилось отношение к своей жизни у Гурова, после того...
2 - Как меняется степень окисления при окислении?Почему?...
2 - Подготовиться к туристскому походу, правильно распределив снаряжение между...
3 - Выберите правильные варианты: Оксид железа(2) в отличие от оксида железа(3)...
2