Как нарисовать солнышко с графиков функций? особенно непонятно, как отрезки должны выглядеть. сказали - через объединение.

Ответы

pziipzii 13.06.2020 03:15

Совокупность таких уравнений определит лучики солнышка:

у=1/2*x

y=x

y=2x

y=-2x

y=-x

y=-1/2*x

ПОКАЗАТЬ ОТВЕТЫ

roxolanavarLana 13.06.2020 03:15

x^2+y^2 = r^2 , задаёт окружность радиуса r

Что бы задать лучи, используем несколько функций вида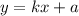 y = kx + a

При a = 0, все прямые, задаваемые уравнениями вида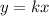 y = kx , будут проходить через точку пересечения координатных осей.

Возьмём 5 прямых, которые будут иметь угол с осью Ох, соответственно, в 0, 30, 60,120, 150 градусов. Этим углам соотвествуют следующие значения углового коэффициента k: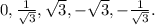 $0, \frac{1}{\sqrt{3}}, \sqrt{3}, -\sqrt{3}, -\frac{1}{\sqrt{3}}.$ Под углом 90 градусов будет падать прямая x = 0.

$y = 0, y = \frac{1}{\sqrt{3}}x, y = \sqrt{3}x, y = \sqrt{3}x, y = \frac{1}{\sqrt{3}}x, x = 0.$

Осталось вырезать у этих прямых отрезки, которые лежат внутри окружности. Для этого найдём точки пересечения этих прямых и окружности.

$1) y = 0, x^2 = r^2, x = r, x = -r.\\ 2) y = \frac{1}{\sqrt{3}}x, 4x^2=3r^2, x = \frac{\sqrt{3}r}{2}, x = -\frac{\sqrt{3}r}{2}\\ 3) y = \sqrt{3}x, 4x^2=r^2, x = \frac{r}{2}, x = -\frac{r}{2}\\ 4) y = -\sqrt{3}x, 4x^2=r^2, x = \frac{r}{2}, x = -\frac{r}{2}\\ 5) y = -\frac{1}{\sqrt{3}}x, 4x^2=3r^2, x = \frac{\sqrt{3}r}{2}, x = -\frac{\sqrt{3}r}{2}\\ 6) x = 0, y^2 = r^2, y = r, y = -r.$

Тогда:

$(x^2+y^2 = r^2) \cup (y=0, x \in (-\infty, -r]\cup[r, +\infty)) \cup\\ (y=\frac{1}{\sqrt{3}}x, x \in (-\infty, -\frac{\sqrt{3}r}{2}]\cup[\frac{\sqrt{3}r}{2}, +\infty))\cup\\(y=\sqrt{3}x, x \in (-\infty, -\frac{r}{2}]\cup[\frac{r}{2}, +\infty))\cup\\(y=-\sqrt{3}x, x \in (-\infty, -\frac{r}{2}]\cup[\frac{r}{2}, +\infty)\cup\\(y=-\frac{1}{\sqrt{3}}x, x \in (-\infty, -\frac{\sqrt{3}r}{2}]\cup[\frac{\sqrt{3}r}{2}, +\infty))\cup\\(x=0, y \in (-\infty, -r]\cup[r, +\infty))$