Известно что 4x^2-4xy+3y^2/2y^2+2xy-5x^2=1 вычислите x+y/x-y . Можно быстрее
Другие вопросы по теме Алгебра
Популярные вопросы
- Кут між висотами паралелограма,проведеним з вершини тупого кута...
3 - На каком расстоянии от собирающей линзы нужно поместить предмет,...
2 - Найдите инфимум и для множества { (( − 1 )^n)*((1/4) − 2/n ) : n...
1 - Решите уравнение 2sin(п+x)=sin2x-3sin^3 x...
1 - По произведению пушкина евгений онегин написать отзыв сначала о...
1 - Заранее органоид, участвующий в делении клетки, равномерном распределении...
1 - Сопротивление внешней части замкнутой цепи равно внутреннему сопротивлению...
3 - Надо. к отряду куриных относятся а) улар, фазан b) сапсан, орел...
2 - 1| в окружности радиуса 1 проведена хорда длины 1. найти площадь...
3 - На одном станке партию деталей можно изготовить за 5 часов, а на...
1
ответ: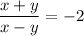 .
.