1. Алгебра
  2. Избавься от иррациональности

Избавься от иррациональности в знаменателе дроби: 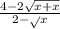\frac{4 - 2 \sqrt{x + x} }{2 - \sqrt{} x}
​

LopsterId1236543 LopsterId1236543    3   13.10.2020 11:38    0

Ответы
student033 student033  13.10.2020 12:01

ответ: Иэбавиться от иррацио

нальности в знаменателе дроби.

\frac{8 + x \sqrt{x} }{4 - x}

Объяснение:

\frac{4 - 2 \sqrt{x} + x }{2 - \sqrt{x} } = \frac{4 - 2 \sqrt{x} + x}{2 - \sqrt{x} } \times \frac{2 + \sqrt{x} }{2 + \sqrt{x} } =

= \frac{(2 + \sqrt{x})(4 - 2 \sqrt{x } + x) }{(2 - \sqrt{x})(2 + \sqrt{x} ) } =

= \frac{ {2}^{3} + ( { \sqrt{x} )}^{3} }{ {2}^{2} - ( { \sqrt{x} })^{2} } = \frac{8 + \sqrt{x \times {x}^{2} } }{4 - x} =

= \frac{8 + \sqrt{x} \times {( \sqrt{x}) }^{2} }{4 - x} = \frac{8 + x \sqrt{x} }{4 - x}

В числителе применяем обратную

формулу суммы кубов, а в знамена

теле обратную формулу разности

квадратов.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
linvliv linvliv  04.11.2019 21:08
решить примеры по логарифмам, степеням и корням, ....
Neal12 Neal12  04.11.2019 21:08
Решите уровнение: в) 17р-8-(р+7)+15=0г) 6m-4)-(7m+7)-m=1​...
MARI5368334 MARI5368334  04.11.2019 21:05
Решить показательное уравнение !...
Кея1563 Кея1563  04.11.2019 20:59
На площині накреслені два круги, радіуси яких 7 і 10 відповідно. знайти ймовірність того, що точка, кинута навмання у великий круг, попаде в кільце, яке утворилось даними кругами....
влада415 влада415  04.11.2019 20:56
Решите уравнения и найдите корень, ​...
lebedko2004 lebedko2004  24.06.2019 17:20
Найдите наименьшее значение квадратного трехчлена a^2-4a+7...
1660044 1660044  24.06.2019 17:20
Найдите радиус описанной около правильного треугольника окружности если стороны треугольника равны (5 корней из 3)...
Chernysh14 Chernysh14  24.06.2019 17:20
Вычислить площадь фигуры ограниченной линиями y=0 x=4 y= корень из x...
guka070806 guka070806  24.06.2019 17:20
Найдите корни уравнения x^4-10x^2+9=0...
Соня135135 Соня135135  21.04.2019 18:56
Решите неравенство x^2-4x+3 0​...

Популярные вопросы