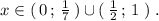Интересное логарифмическое неравенство.
Другие вопросы по теме Алгебра
Популярные вопросы
- Почему Наполеон не смог остаться при власти?...
3 - Смешали воду массой 1780г, имеющую температуру 25 °С, и воду при температуре...
1 - Укажите решение неравенства 3 × (5 — 7x) 9 – 11т.х...
3 - Визначіть присудки в реченнях та вкажіть іх вид ( речення можна не...
3 - в одном из произведений пушкина текст которого приведен в подкаталоге...
2 - Массив С(10) заполнен случайным образом в интервале (-10, 10). Найти...
2 - Какие географические открытия были сделаны в 16-17 веках? ...
3 - Warum Mülltonen bunt sind Die Mülltonnen in Deutschland haben alle...
2 - 3 во 2 степени умножить на 8 в 3 степени и умножить на 9...
3 - Фонетичний розбір слова Прислів я ...
3
ответ: во вложении Объяснение:
Метод рационализации. Заменяем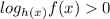 на произведение
на произведение
Основания логарифмов меньше 1, поэтому логарифмы - убывающие функции, значит
Учитывая ОДЗ имеем
Рассмотрим , когда основание логарифмической функции больше 1 , и когда оно находится в пределах от 0 до 1 . Соответственно этому запишем пределы изменения аргумента логарифма.
С учётом ОДЗ, получим тот же ответ: