(Хотя бы один пример , просто чтобы понять как это делать)
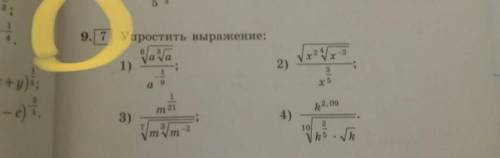
Другие вопросы по теме Алгебра
Популярные вопросы
- Вравностороннем треугольнике авс со стороной, равной 6 см, точки...
1 - Найдите сложноподчиненное предложение с последовательным подчинением...
2 - Причина вступления в войну шведции 1618-1648...
2 - Спільнокореневі слова до слів зерно, береза...
1 - Сказка хуха- моховынка глупая или нет...
2 - Составить текст на украинском языке на тему: постукала осінь до мене...
1 - Как в лексикологии называются слова братца и браться?...
2 - (sqrt- квадратный корень) : sqrt(3x+1) ( /=) 0...
1 - Уравнение реакции 1) галогенирование пропилена, 2) гидрогалогенирование...
1 - Составь логическую схему для ответа на вопрос верно ли, что, если...
1
Відповідь:![\sqrt[3]{а}](/tpl/images/3868/9116/7ce43.png)
Пояснення:
Объяснение: