Хочу чтобы вы решили 4-й пример этим же и обьяснили вторую строку почему там появилась 9-1/9-1*(9+1)
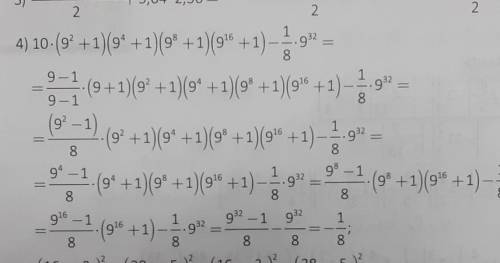
Другие вопросы по теме Алгебра
Популярные вопросы
- основи прямокутної трапеції дорівнюють 3 і 5 см знайдіть площу прямокутної...
1 - Лисица 1) (-3:0).(-2: 1), (3; 1). (3:2).(5:5). (5:3). (6:2),(7:2), (7:1.5),(5:0),...
3 - Сколько грамм воды получится, если разложили при нагревании 23,4 г гидроксида...
3 - Где можно скачать « чертіщева фізика 7 клас зошит для поточного та тематичного...
3 - Сравните Давань и Кингха.please ...
3 - G(x)=|x−15|+2 та f(x)=(x+2)2+6. Обчисли g(x)+f(x), якщо g(−33);f(1)....
2 - 22. Сравните Великобританию и Индию. ПоказателиДля сравненияВеликобританияИндияГеографическоеIіоложениеПлощадь,...
3 - 1.предлог- а) самостоятельная часть речи б) особая часть речи в)служебная...
1 - Номер 1345 6 класс 2 часть учебника ....
3 - Какая из проволок, платиновая или золотая (одинакового сечения), нагревается...
1
Число 10 можно представить в виде:
Это делают для того, чтобы получить множитель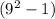 , так как тогда далее получим произведение
, так как тогда далее получим произведение 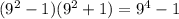 . И так далее ...
. И так далее ...
В принципе можно сразу заметить, что сумму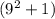 так и хочется умножить на разность
так и хочется умножить на разность 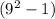 , чтобы воспользоваться формулой разности квадратов . Но если умножить выражение на такую разность, то сразу же надо и разделить на эту разность, чтобы не изменить заданное выражение. Получим
, чтобы воспользоваться формулой разности квадратов . Но если умножить выражение на такую разность, то сразу же надо и разделить на эту разность, чтобы не изменить заданное выражение. Получим