1. Алгебра
  2. Given 3x+y = 12, find

Given 3x+y = 12, find the maximum value of x^2 −y^2

Асем1211 Асем1211    1   30.05.2023 13:13    0

Ответы
404ada505 404ada505  30.05.2023 13:14

ответ:  max( x²- y²) = 18   при  3х+у=12  .

Переменные  х  и  у  связаны соотношением   3х+у=12  .

Найти максимальное значение выражения   x²-y²  .

\bf 3x+y=12\ \ \ \Rightarrow \ \ \ y=12-3xx^2-y^2=x^2-(12-3x)^2=x^2-144+72x-9x^2=-8x^2+72x-144  

Найдём максимальное значение выражения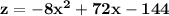  \bf z=-8x^2+72x-144  .

\bf z=-8(x^2-9x+18)\ \ ,\ \ \ z=-8\, (x-6)(x-3)

\bf z'=-8\cdot 2x+72=-8\cdot (2x-9)=0\ \ ,\ \ 2x=9\ \ ,\ \ x=4,5    

В стационарной точке функция  z  будет принимать максимальное значение, так как при переходе через  х = 4,5 знак производной z' меняется с плюса на минус :    + + + + + [4,5 ] - - - - -    \bf x_{max}=4,5  

Подставим значение  х = 4,5 в выражение .

\bf z(4,5)=-8\, (4,5-6)(4,5-3)=-8\cdot (-1,5)\cdot 1,5=18(x^2-y^2)\Big|_{x=4,5}=18              


Given 3x+y = 12, find the maximum value of x^2 −y^2
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
nmoskvich nmoskvich  07.03.2019 21:00
Докажите что при любых значениях переменных многочлен x^2+2x+y^2-4y+5 принимает неотрицательные значения...
яна2754 яна2754  07.03.2019 21:00
Расставьте вместо вопроса знаки арифметических операций(минус, плюс, умножить, разделить) так, чтобы были верны следующие равенства в двоичной системе счисления: а) 1100...
staskostenko1 staskostenko1  07.03.2019 21:00
Найдите уравнение касательной к графику функции f(x)=sqrtx, которая паралельна прямой заданной у=x-5...
Igor20018 Igor20018  07.03.2019 21:00
Выражение корень из 5 * корень из 28 все / на корень из 10...
VernerIgor VernerIgor  07.03.2019 21:00
Решите неравенство: 4sinxcosx 1...
dianakokorina91 dianakokorina91  07.03.2019 21:00
Решите уравнение: 1) x (в квадрате) -19x+16=0 2) x (в квадрате) -15x+36=0 3) 36x (в квадрате) -12x+1=0...
Бесконечноенебо Бесконечноенебо  07.03.2019 21:00
Найдите площадь равнобедренноц трапеции если ее меньшее основание равно 7см боковая сторона- 13см высота-12см...
anitabadurova anitabadurova  07.03.2019 21:00
Решите уравнение: 1)-7x (в квадрате) +13=0 2)2x(в квадрате)-18=0 3)x(в квадрате)+2x=0 4)4x(в квадрате)=0 5)7x+3=2x(в квадрате)+3x+3...
Саша99990 Саша99990  07.03.2019 21:00
Построить график функции y=x^2-6x+5 и найти её наименьшее значение....
Kto6to Kto6to  07.03.2019 21:00
Николай на выполнение работы по затратил на 30 мин больше, чем по . всего на эти два предмета он затратил 1 ч 40 мин. сколько времени потребовалось на каждый предмет?...

Популярные вопросы