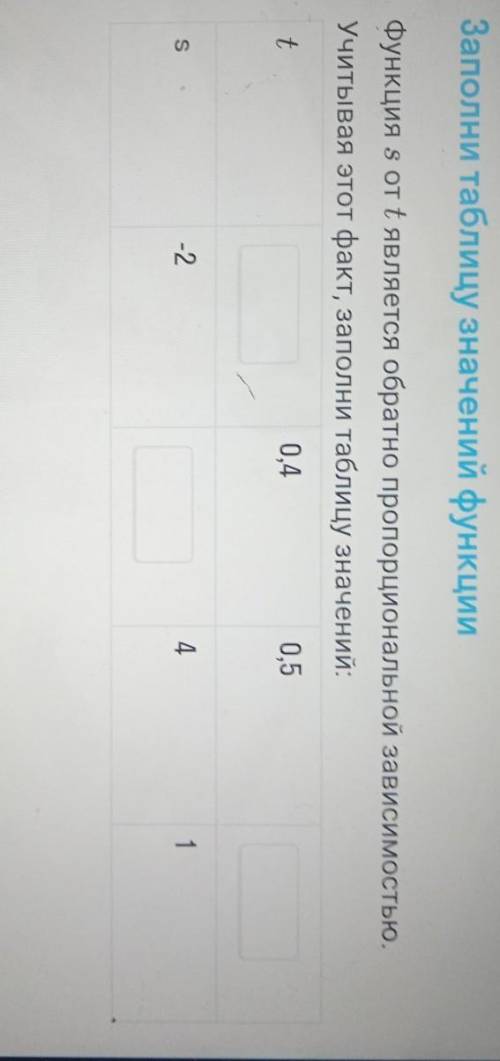
Функция s от t является обратно пропорциональной зависимостью учитывая этот факт, заполни таблицу
Другие вопросы по теме Алгебра
Популярные вопросы
- Краткий рассказ на тему один день из жизни князя,,...
2 - Виберіть з переліку алкіни...
3 - Яку роботу слід виконати, щоб із колодязя глибиною 10 м підняти відро з водою...
1 - длина детали на чертеже, изготовленном в масштабе 1:5, равна 7,2 см.чему будет...
2 - До іть вирішити дане запитання номер 4 буль даска...
1 - ЗАВДАННЯ 5 ( ). Для визначення питомої теплоти плавлення свинцю розплав- лений...
3 - 3. Подпиши, кто сделал эти запасы на зиму...
3 - ОВР Zn+H2SO4⇒ZnSo4 + So2↑+H2O...
3 - 1обведи синим цветом источники пресной воды. Море, река, океан, озеро Алаколь,...
2 - 3. Объясните, по какому принципу образован ряд и какую роль сыграли указанные...
3
В данном случае, функция s от t является обратно пропорциональной зависимостью, что означает, что чем больше значение t, тем меньше будет значение s, и наоборот.
Теперь давайте заполним таблицу:
Если мы посмотрим на значения, то заметим следующую закономерность: когда t удваивается (т.е. умножается на 2), s уменьшается вдвое. Это свойство обратно пропорциональной зависимости.
Давайте посчитаем значения для таблицы:
1. Когда t=4, мы знаем, что s=5. Соответствующее значение s мы находим, деля 20 (начальное значение s) на 4 (начальное значение t): 20/4 = 5.
2. Когда t=8, мы можем использовать ранее установленное свойство обратно пропорциональной зависимости, чтобы найти s. Таким образом, мы знаем, что когда t удваивается, s уменьшается вдвое. То есть, если мы умножаем 4 (начальное значение t) на 2, чтобы получить 8, то s должно быть уменьшено вдвое. Изначально s=5, поэтому 5/2=2.5.
3. Когда t=12, мы можем использовать тот же принцип. Теперь мы должны умножить 4 (начальное значение t) на 3, чтобы получить 12, и, следовательно, s должно быть уменьшено втридорого. Изначально s=5, поэтому 5/3=1.67.
4. И, наконец, когда t=16, мы должны умножить 4 (начальное значение t) на 4, чтобы получить 16, следовательно, s должно быть уменьшено вчетыре раза. Изначально s=5, поэтому 5/4=1.25.
Таким образом, заполняя таблицу, мы получаем следующие значения:
t | s
-------
4 | 5
8 | 2.5
12 | 1.67
16 | 1.25
Надеюсь, эта подробная информация и пошаговое объяснение помогли вам понять, как заполнять таблицу в случае обратно пропорциональной зависимости. Если у вас остались вопросы, пожалуйста, не стесняйтесь задавать.