F(x) =3x^3+5x^2-3
f'(x) =0
f'(x) <0
Другие вопросы по теме Алгебра
Популярные вопросы
- Из пункта а в пункт в выехал автобус со скоростью 45км/ч.спустя1...
3 - Скакой силой взаимодействуют в вакууме два точечных электрических...
2 - Составьте предложения, в которых с этими прилагательными употребляя...
1 - На сколько изменится температура воды,масса которой 22кг. ,...
3 - Найти удельную теплоёмкость кислорода при v=const при p=const?...
1 - Почему мышцы красные, а сухожилия белые?...
2 - На цоколе элекстрической лампочки написано 6,3в; 0,28а. найдите...
1 - Какая сила действует на протон, движущийся со скоростью 2*10^6...
2 - Эссе на тему: любая война - это всегда трагедия.но трагедия...
1 - С! : 1) используя формулы , тригонометрические выражения к функциям...
1
Объяснение:
На основе решения уравнения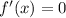 воспользуемся методом интервалов для решения неравенства (смотрите рисунок):
воспользуемся методом интервалов для решения неравенства (смотрите рисунок):