1. Алгебра
  2. F(x)= 1/ квадратный корень

F(x)= 1/ квадратный корень из 2х- х2 (в квадрате) найти область определения функции

Lililililililiza Lililililililiza    2   15.03.2019 07:30    2

Ответы
hromovaalyona2 hromovaalyona2  25.05.2020 11:55

На ноль делить нельзя; подкоренное выражение должно быть неотрицательным.

Для функции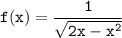 \tt \displaystyle f(x)=\frac1{\sqrt{2x-x^2 }} :

\displaystyle \begin{Bmatrix}\sqrt{2x-x^2 } \ne 0\\ 2x-x^2 \ge 0\end{matrix} \quad \begin{Bmatrix}2x-x^2\ne 0\\ 2x-x^2 \ge 0\end{matrix} \\ \\ 2x-x^20\; \;\; \begin{vmatrix} \\\end{matrix} \cdot ($-$1)<0\\ \\ x^2-2x<0\\ x(x-2)<0

Решим методом интервалов.

x∈(0;2)

ответ: D(f) = (0;2).

Для функции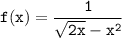 \tt \displaystyle f(x)=\frac1{\sqrt{2x} -x^2 }} :

\displaystyle \begin{Bmatrix}\sqrt{2x} -x^2 \ne 0\\ 2x\ge 0\qquad \end{matrix} \quad \begin{Bmatrix}\sqrt{2x} \ne x^2 \\ x\ge 0\quad \end{matrix} \\ \\ \begin{Bmatrix}2x\ne x^4 \ge 0\\ x\ge 0\qquad \end{matrix} \quad \begin{Bmatrix}x(x^3 -2)\ne 0\\ x\ge 0\qquad \end{matrix} \\ \\ \begin{Bmatrix}x\ne \{ 0;\sqrt[3]2\} \\ x\ge 0\qquad \end{matrix}

\displaystyle x\in (0;\sqrt[3]2)\cup (\sqrt[3]2 ;+\infty )

ответ: \tt \displaystyle D(f)=(0;\sqrt[3]2)\cup (\sqrt[3]2 ;+\infty ).


F(x)= 1/ квадратный корень из 2х- х2 (в квадрате) найти область определения функции
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
neganov neganov  11.07.2019 11:40
На клетчатой плоскости закрашена одна клетка. каждую минуту клетка закрашивается, если она граничит по стороне сзакрашенной клеткой. сколько клеток будет закрашено через...
kruglov428 kruglov428  11.07.2019 11:40
Умножение многочленов (3x-4y)(3x+4y) (5p+6q)(6q-5p) (-7a+1)(1-7a)...
котик8308 котик8308  11.07.2019 11:40
Вычислить площадь фигуры ограниченной линиями...
buschckovaanas buschckovaanas  11.07.2019 11:40
(-3а-10в)^2 формулы сокращенного умножения...
никусь2222 никусь2222  11.07.2019 11:40
Дано: d=4, an=50, sn=330. найдите а1 и n...
derek56 derek56  11.07.2019 11:40
Разложить на множители. a^n-a^m n m на 3...
DashkaaMilashka DashkaaMilashka  02.12.2020 17:41
Построить график функции у=-2х-4 а) Принадлежит ли графику точка В(-20;-70) б) Указать с графика значение х при котором у=6; у=0...
Khamidullovaals Khamidullovaals  02.12.2020 17:41
Взаимосвязь графиков линейных функций. Урок (-4; -16) 3 у = 4х - 4. y = –4x + 4. у = 6х + 8. у = 6х - 13....
virina059 virina059  02.12.2020 17:41
каждую пятницу, начиная с 8 января 2021 года, Пётр Семёнович планирует практиковаться в стрельбе по следующей схеме: в первую тренировку израсходовать 60 патронов, а на...
evasyperandreev evasyperandreev  02.12.2020 17:41
Sin2x+√3*cos2x = -1 = - Больше или равно...

Популярные вопросы