1. Алгебра
  2. Есть простое выражение: 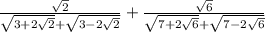Решение

Есть простое выражение: \frac{\sqrt{2} }{\sqrt{3+2\sqrt{2} } + \sqrt{3 - 2\sqrt{2} } } + \frac{\sqrt{6}}{\sqrt{7 + 2\sqrt{6} } + \sqrt{7 - 2\sqrt{6} }}

Решение вроде очевидное:


Это насколько меня хватает... Далее если взять калькулятор и посчитать, то ответ приблизительно 1,11. Официальная же версия ответа 1. Очевидно что где-то скрывается недоумение и я его не вижу... Кто-нибудь может подсобить с этим?


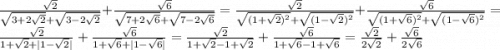
\frac{\sqrt{2} }{\sqrt{3+2\sqrt{2} } + \sqrt{3 - 2\sqrt{2} } } + \frac{\sqrt{6}}{\sqrt{7 + 2\sqrt{6} } + \sqrt{7 - 2\sqrt{6} }} = \frac{\sqrt{2} }{\sqrt{(1+\sqrt{2} )^{2} } + \sqrt{(1-\sqrt{2} )^{2}}}+\frac{\sqrt{6}}{\sqrt{(1+\sqrt{6})^{2}}+ \sqrt{(1-\sqrt{6} )^{2}}} = \frac{\sqrt{2} }{1+\sqrt{2}+|1-\sqrt{2} |} + \frac{\sqrt{6}}{1+\sqrt{6} + |1-\sqrt{6}|} = \frac{\sqrt{2} }{1+\sqrt{2}-1+\sqrt{2}} + \frac{\sqrt{6}}{1+\sqrt{6} -1+\sqrt{6}} = \frac{\sqrt{2}}{2\sqrt{2}}+\frac{\sqrt{6} }{2\sqrt{6}}
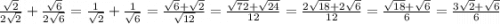
\frac{\sqrt{2}}{2\sqrt{2}}+\frac{\sqrt{6} }{2\sqrt{6}} = \frac{1}{\sqrt{2}}+\frac{1 }{\sqrt{6}} = \frac{\sqrt{6} + \sqrt{2} }{\sqrt{12}} = \frac{\sqrt{72} + \sqrt{24} }{12} = \frac{2\sqrt{18} +2\sqrt{6} }{12} = \frac{\sqrt{18} +\sqrt{6} }{6} = \frac{3\sqrt{2} +\sqrt{6} }{6}

Nikolayal Nikolayal    1   13.04.2021 22:18    0

Ответы
Показать ответы (3)
Другие вопросы по теме Алгебра
miqwq miqwq  20.09.2019 14:20
Взаимное расположение графиков линейных функций (при каких условиях графики параллельны, , пересекаются)....
isa2221 isa2221  20.09.2019 14:20
Решить уравнение sin ( -3pi/2) + cos pi/4 , покажите еще решение...
anya071101 anya071101  20.09.2019 14:20
Как найти наибольшее и наименьшее значения функции?...
Ira1214 Ira1214  20.09.2019 14:20
Постройте график у=х^2-6х+7. найдите по графику: а) у(-2)= б) промежутки возрастания и убывания функции , хелпи ми, плез...
nik868 nik868  20.09.2019 14:20
Площадь прямоугольника 56 кв. см., его длина 9см. найди периметр...
polinaasya polinaasya  20.09.2019 14:20
Прилагательное в предложении всю зиму кормитсявыхухоль на своих подводных пастбищах употреблено в форме м.р , с.р. ж.р. множественного числа...
benten2434 benten2434  20.09.2019 14:20
Моторная лодка проплывет 49 км против течения реки и 8 км по озеру затратив на весь путь 2 часа найдите собственную скорость лодки если скорость течения реки составляет...
wondermang wondermang  20.09.2019 14:20
Найти сумму первых восьми членов прогрессии : -2; q=-3...
ниёля1 ниёля1  20.06.2019 05:50
Какое из следующих выражений равно 5^k-3 1) 5^k/5^3 2)5^k/5^-3 3) 5^k-5^3 4) (5^k)^-3...
Galina1960 Galina1960  20.06.2019 05:50
При каком значении x значение дроби: 1) х-1 / х+4 равно 0; 2; 3/2; -3/2?...

Популярные вопросы