Докажите, что уравнение 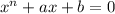имеет не больше 3 корней.

Объяснение:

Количество корней будет завесить от количества экстремумов функции.

У функции уравнения с тремя корнями должно быть два экстремума, у функции с четырьмя конями  должно быть три экстремума.

Чтобы найти экстремумы берём производную.

решением такого уравнения может быть один (в случае если n - нечётное число) или два (в случае если n - чётное число) корня.

Но три корня быть не может, следовательно эта функция имеет или один экстремум и максимум два корня или два экстремума и максимум три корня.