Докажите, что при любом натуральном n число 3 в степени n + 2(n+ 1) + 5 в степени n делится на 4
Другие вопросы по теме Алгебра
Популярные вопросы
- Выделите причастие , укажите в каждой строчке его отличительный признак....
1 - Как решить пример 11м27см÷7 в столбик...
1 - Смешали 2 раствора одной и той же соли: 180г 10% и 250г 15%. найти массовую...
1 - Напишите на сочинение на тему зимние каникулы с переводом...
2 - язык найти из : 1 предложение простое 2 предложение с/с(сложно сочин)...
3 - Какам словом можно заменить слово жевучей...
2 - Реферат с планом и выводом на тему: гигиена девочки...
1 - Нужна песня с упоминанием любого цвета.буду выступать перед всей школой...
3 - Rboh растворимое или не растворимое основание?...
1 - Значение фразеологизма палка о двух концах о делах...
3
Для доказательство просто рассмотрим два случая: когда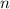 - нечетное и когда
- нечетное и когда 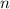 - четное.
- четное.
1).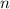 - нечетное, то есть
- нечетное, то есть 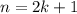 .
.
При всех нечетных натуральных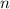 число
число 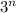 имеет остаток
имеет остаток 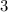 при делении на
при делении на 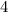 .
.
Доказать это можно таким образом: приТакже, при любом натуральном значении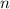 число
число 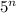 имеет остаток
имеет остаток  при делении на
при делении на 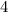 .
.
Так происходит, потому что само числоТретье слагаемое: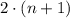 будет нацело делиться на
будет нацело делиться на 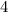 :
:
Значит, если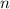 - нечетное, то:
- нечетное, то:
При нечетных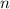 все, как видите, сходится.
все, как видите, сходится.
2).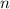 - четное, или же
- четное, или же 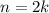 .
.
Как мы определили ранее, в этом случае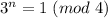 и
и 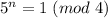 .
.
При этом второе слагаемое:
Найдем всю сумму:
И при четных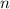 утверждение работает.
утверждение работает.
Как известно, каждое натуральное число либо четное, либо нечетное (третьего не дано) и никаких других натуральных чисел, которые не являются четными и не являются нечетными одновременно, науке неизвестно.
Так что мы рассмотрели все случаи, и в каждом из них результат был равен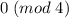 , то есть делился на
, то есть делился на 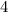 .
.