1. Алгебра
  2. Докажите, что если 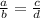то

Докажите, что если \frac{a}{b} =\frac{c}{d} то верны следующие производные пропорции: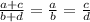 \frac{a+c}{b+d} =\frac{a}{b} =\frac{c}{d}

valera212105 valera212105    1   17.08.2020 14:19    2

Ответы
YDA2007 YDA2007  15.10.2020 16:00

Если верна пропорция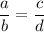 \dfrac{a}{b} =\dfrac{c}{d}, то по основному свойству пропорции произведение крайних членов равно произведению средних членов:

ad=bc

Рассмотрим пропорцию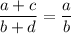 \dfrac{a+c}{b+d} =\dfrac{a}{b}. Проверим, равно ли произведение крайних и произведение средних членов:

(a+c)\cdot b=(b+d)\cdot a

ab+bc=ab+ad

Слагаемое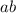 ab взаимно уничтожается.

bc=ad

Это равенство верно, так как оно получено из исходной верной пропорции.

Рассмотрим пропорцию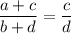 \dfrac{a+c}{b+d} =\dfrac{c}{d}. Проверим, равно ли произведение крайних и произведение средних членов:

(a+c)\cdot d=(b+d)\cdot c

ad+cd=bc+cd

Слагаемое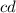 cd взаимно уничтожается.

ad=bc

Это равенство также верно, так как оно получено из исходной верной пропорции.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Kotumi Kotumi  17.12.2020 09:06
А) 5^2*5^3; б) 8^8/8^3; в) (b^4)^5; г) 3^7*4^7...
Millat23 Millat23  17.12.2020 09:06
ответы записать : 1); 2); 3);...; и т.д​...
evaklchn evaklchn  17.12.2020 09:05
Витя пропалывает картофельную борозду за 12 минут, а его друг Олег такую же самую борозду пропалывает за 60 минут. Сколько времени потребуется обоим друзьям, чтобы вместе прополоть...
arhangel33 arhangel33  17.12.2020 09:04
Решите неравенство (3/7)^2x+1 9/49...
айрат36 айрат36  17.12.2020 09:03
2 в четвертой степени * ab²(-1/2)³ * a²b=?...
Kesha4444 Kesha4444  17.12.2020 09:03
3х2 – 2x = 0 x ( 3х – 2) = 0х = 0 или3х - 2 = 03x =? Я тупень(​...
ygthjkujny ygthjkujny  17.12.2020 09:03
Упростите выражение А) А+С,Б) D-В,В) В ◌ּ D,Г) А ◌ּ В – С ◌ּ D,где А =х2-3х+2, В= 2х+5, С= 2х2+7х+17, D=х-4.Очень нужно...
antihype3 antihype3  17.12.2020 09:02
Замени * одночленами, чтобы равенство было верным: k*-50 u²n⁴ + 125uh⁵= 5uh3=4u²-*+*​...
kobyarova2001 kobyarova2001  17.12.2020 09:02
сума двох чисел дорівнює 14, а) якого найбільшого значення може набувати добуток цих чисел? б) якого найменшого значення може добувати сума квадратів цих чисел?​...
топфифа2 топфифа2  17.12.2020 09:01
Радиус земного шара равен 6370 км. Вычислите объем земли, площадь поверхности, площадь суши ( примерно 29% площадиповерхности).( Справочно: объем шара вычисляется по формуле:...

Популярные вопросы