1. Алгебра
  2. Докажите что 3^n+2 - 2^n+2

Докажите что
3^n+2 - 2^n+2 + 3^n - 2^n
делится на 10

AnnHaylen AnnHaylen    3   21.01.2020 16:17    1

Ответы
elenchik2006 elenchik2006  11.10.2020 02:12

3^{n+2}-2^{n+2}+3^{n}-2^{n}=(3^{n+2}+3^{n})-(2^{n+2}+2^{n})=3^{n}(3^{2}+1)-2^{n-1} (2^{3}+2)=3^{n}*10-2^{n-1}*10=10*(3^{n}-2^{n-1})

Если один из множителей делится на 10, то и всё произведение делится на 10.

ПОКАЗАТЬ ОТВЕТЫ
svetlanko2000 svetlanko2000  11.10.2020 02:12

Объяснение: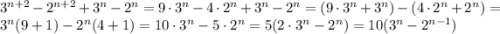  3^{n+2}-2^{n+2}+3^n-2^n=9\cdot3^n-4\cdot2^n+3^n-2^n=(9\cdot3^n+3^n)-(4\cdot2^n+2^n)=3^n(9+1)-2^n(4+1)=10\cdot3^n-5\cdot2^n=5(2\cdot3^n-2^n)=10(3^n-2^{n-1})

Очевидно, что полученное выражение делится на 10, что и требовалось доказать.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
kolopok kolopok  01.06.2019 13:00
Представьте в виде произведения многочленов: a(b--2c)...
MartKsenka MartKsenka  01.06.2019 13:00
Найдите сумму первых четырех членов прогрессии если b1=12 , q=-0.5...
Акакий55 Акакий55  01.06.2019 13:10
Выражение: 1/[email protected][email protected]/[email protected]...
Appledog Appledog  01.06.2019 13:10
(sin a+cos a)2 + (sin a - cos a)2=2...
egorkozlovcev egorkozlovcev  01.06.2019 13:10
Докажите тождества: sin α 1+cos α ―― = ―――― 1-cos α sin α...
истоиия истоиия  12.12.2020 02:45
С точки за пределами плоскости найдите проекцию первого откоса 21 см на эту плоскость с двумя откосами длиной 29 см и 25 см.​...
veseloffgleb veseloffgleb  12.12.2020 02:44
№ 3.145 Дана функция у = . Заполните таблицу.х-4-2-1-0,5 -0,25   4у- 1-2  -16 842  у = = = - 1 - 2 =        х = 4 : (- 2) = -2​...
Olgaekolesnik Olgaekolesnik  18.12.2021 01:18
Укажите неравенство, а) которое не имеет решений б) решением которого является любое число. 2 задание...
ника2552 ника2552  18.12.2021 01:28
Функции! Нужно найти Область значень Область визначеннь,интервал роста,интервал падения f(x)={x2−1, якщоx∈[−3;2] √x-1(корень закончился)+2, якщоx ∈(2;5]...
apiloota apiloota  18.12.2021 01:36
Розв’яжіть рівняння: lg(100x) · lg(0,01x) = lg( 1/x²) - 1...

Популярные вопросы