Доказать тождество (√a+√b)/(√a-√b)+(√a-√b)/(√a+√+b)/(a-b)=-1
Ответы
(√a+√b)/(√a-√b)+(√a-√b)/(√a+√b)-(3a+b)/(a-b)=-1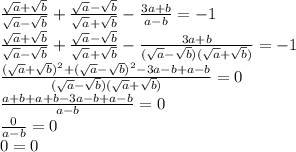
ПОКАЗАТЬ ОТВЕТЫ
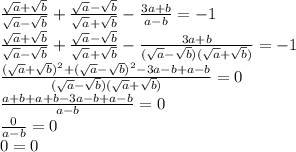
Другие вопросы по теме Алгебра
Популярные вопросы
- Выбранное событие(процесс) а) внешняя политика первых русских князей...
2 - Вычислите объем кислорода, если в результате реакции 2SO2+O2=2SO3...
3 - 7 классВ отеле Санкт-Петербурга есть 2-местные и 3-местные номера,...
1 - Твір на тему чудовий світ Мумі-тролів...
3 - Охарактеризуйте главного героя (Настю) из произведения Кладовая...
1 - Синтаксический разбор предложений: 1. Прилежащий ко двору сад цветёт...
2 - Установіть послідовність подій у творі «Лісова пісня». A мавка до...
1 - ЗА ЗАДАЧУ ПО ХИМИИ! Яку масу технічного кальцій карбіду масова частка...
2 - Какие отличительные черты имеет цветок Однодольных?...
3 - 10. Поставте розділові знаки,накресліть схему,повний синтаксичний...
3