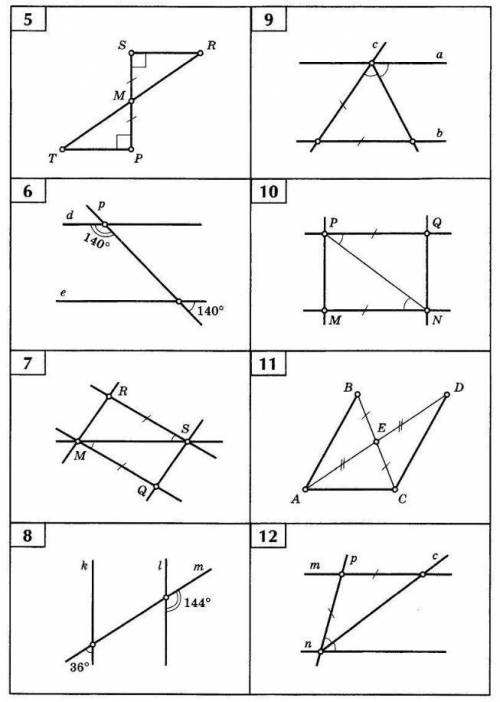
Доказать параллельность прямых №8,9,10,11,12

Для доказательства параллельности прямых №8, 9, 10, 11, 12, нам понадобится использовать следующие свойства параллельных прямых и свойства углов.

1. Свойство: Если две прямые пересекаются третьей прямой так, что сумма внутренних углов по одну сторону равна 180 градусам, то эти две прямые параллельны.
Это свойство называется "признаком соответственных углов".

2. Свойство: Если две параллельные прямые пересекаются третьей прямой, то все соответственные углы равны.
Это свойство называется "признаком параллельных прямых".

Теперь перейдем к доказательству параллельности прямых №8, 9, 10, 11, 12:

1. По данному изображению мы видим, что прямая №10 параллельна прямой №8. Это можно сказать, так как угол между ними (Угол 8) и угол под ними (Угол 10) равны (признак параллельных прямых).

2. Также мы видим, что прямая №12 параллельна прямой №10. Это можно сказать, так как угол между ними (Угол 10) и угол под ними (Угол 12) равны (признак параллельных прямых).

3. Таким образом, имеем, что прямая №8 параллельна прямой №10 параллельна прямой №12.

4. Рассмотрим прямую №9. Мы видим, что она пересекает прямую №10.

5. Теперь используем признак соответственных углов: Выберем пару соответственных углов - Угол 9 и Угол 10.

6. Заметим, что Угол 9 + Угол 10 = 180 градусов, так как они образуют смежные углы.

7. Следовательно, по признаку соответственных углов прямая №9 параллельна прямой №10.

8. Из пунктов 1 и 7 можно сделать вывод, что прямая №9 параллельна прямой №8 и прямой №10.

9. Далее, рассмотрим прямую №11. Мы видим, что она пересекает прямую №10.

10. Применим те же шаги, что и для прямой №9: выберем пару соответственных углов - Угол 11 и Угол 10, заметим, что они образуют смежные углы, и их сумма равна 180 градусам.

11. По признаку соответственных углов имеем, что прямая №11 параллельна прямой №10.

12. Из пунктов 2 и 11 можно сделать вывод, что прямая №11 параллельна прямой №12 и прямой №10.

13. Наконец, имеем, что прямая №9 параллельна прямой №8, прямая №10, прямая №11 и прямая №12.

Таким образом, мы доказали параллельность прямых №8, 9, 10, 11, 12, используя признаки параллельных прямых и соответственных углов.