1. Алгебра
  2. Доказать, что если а — диагональная

Доказать, что если а — диагональная матрица и все элементы ее главной диагонали различны между собой, то любая матрица, перестановочная с а, тоже диагональна

varvarataraskina varvarataraskina    1   12.10.2019 14:57    16

Ответы
nika55551 nika55551  10.10.2020 06:09

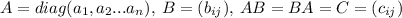
Пусть A=diag(a_1, a_2...a_n),\: B=(b_{ij}),\: AB=BA=C=(c_{ij})

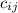Выразим c_{ij} из произведения 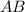AB: c_{ij}=(0\:...\:a_i\:...\:0)*\left[\begin{array}{ccc}b_{1j}\\...\\b_{nj}\end{array}\right] =a_ib_{ij}

Аналогично с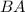 BA: c_{ij}=(b_{i1}\:...\:b_{in})*\left[\begin{array}{ccc}0\\...\\a_j\\...\\0\end{array}\right] =a_jb_{ij}

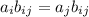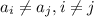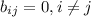Тогда a_ib_{ij}=a_jb_{ij}. Т.к. a_i\neq a_j, i\neq j, то b_{ij}=0, i\neq j, т.е. все элементы, находящиеся не на диагонали, нулевые. А это и означает, что матрица 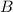B диагональная.

Доказано.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Y563280 Y563280  24.08.2019 04:10
Преобразуйте заданное выражение в многочлен стандартного вида a)-5ab(3а^2-0,2b^2+ab) б)(a+4)(a-5) b)(35a^3b-28a^4): 7a^3...
ADAMREUS ADAMREUS  24.08.2019 04:10
Найдите сумму первых семи членов прогрессии ,если b1=7 ,q=2...
DashaTopjfnfvv DashaTopjfnfvv  24.08.2019 04:10
Sin 7y-sin y= cos 4y решить уравнение...
Miras19932708 Miras19932708  24.08.2019 04:10
При каких значениях х значение функции у=3x^2-5x-2/2-x равно 0...
kril20101 kril20101  24.08.2019 04:10
3x^2-4x=0 решите через дискрименант...
Селена24на7 Селена24на7  24.08.2019 04:10
Хв квадрате минус7 равно 0 найти дискриминант...
alizhanayanaoxi717 alizhanayanaoxi717  20.10.2020 13:24
Точка L (-3;-4) лежить у четвертіА. першійБ. другійВ. третійГ. четвертій​...
Krutoyabrikos Krutoyabrikos  20.10.2020 13:23
Двухчастный дневник цитата комментарий.В правой колонке опредетили какие именно чуство испытывает Бим помигите руский язык 6 класс упр5 стр91 ​...
pelmen123456789 pelmen123456789  20.10.2020 13:23
Найдите область определения функции 84-85...
апркаерн апркаерн  15.04.2020 16:18
Закон движения точки по прямой задается формулой s(t)=3t+8, где t - время (в секундах), s(t) - отклонение точки в момент времени t (в метрах) от начального по­ложения. Найдите...

Популярные вопросы