Доказать, что а+в> (√2011+√2012)², если ,а> 0,в> 0,ав> 2011а+2012в
Ответы
Чуть более нормально ,сделаем замену 2011=x, и докажем в общем
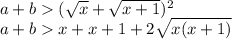
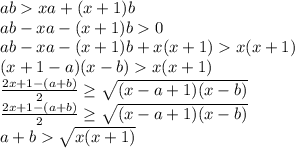
ПОКАЗАТЬ ОТВЕТЫ
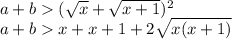
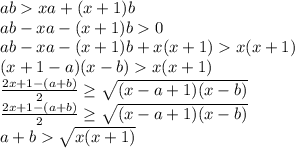
Другие вопросы по теме Алгебра
Популярные вопросы
- Инайдите значения выражений. b+42,7+(39,825-2,74, если b=16,61; d+60,19-(68,7-9,1)...
1 - Сбазы отправили в первый магазин три грузовика муки а в другой 5...
3 - Кразности чисел 59 и 39 прибавить разность чисел 48 и 32...
1 - Использо признаки делимости произведения суммы и разности чисел а...
2 - Следопыт-как ты понимаешь значение слова инкогнито? какова оно рода?...
1 - Грамматика к уроку 42. this is или these are 1. my mother s friend....
2 - Вкаких соединениях ряда h2s,n2,hi,h2,naf,ci2,caf2 степень окисления...
1 - Определить число род склонение и падеж имени существительного ночь...
1 - Что получается при взаимодействии сульфата меди (ii) и сульфата аммония?...
2 - Вмагазин бытовой техники видеокамеры и телевизоры на общую сумму...
3