Алгебра: Доказать, что 4 в восьмой + 2 в тринадцатой делится на 18

Доказать, что 4 в восьмой + 2 в тринадцатой делится на 18

Ответы

hfdgddcju 01.02.2022 06:00

Просто вынесем за скобки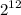 $\displaystyle 2^{12}$ :

$\displaystyle 4^8+2^{13}=(2^2)^8+2^{13}=2^{16}+2^{13}=\\2^{12} \cdot (2^{4}+2)=2^{12} \cdot (16+2)=2^{12} \cdot 18$

Как видим, в ходе преобразований получилось, что один из множителей - число 18, а это значит, что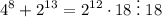 $\displaystyle 4^8+2^{13}=2^{12} \cdot 18\; \vdots \; 18$ . Ч.Т.Д.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

pirishok 16.10.2019 11:24

Найти нули функции и определить четность и нечетность...

АНОНЯ1478 16.10.2019 11:28

Два автомобиля,работая вместе,могут перевезти груз за 15 часов.один автомобиль работал на 6 часов меньше,чем второй,и перевез 40% груза,а второй-оставшийся груз.сколько часов...

ГораСлез 16.10.2019 11:29

Пересекается ли график функции y = √х с прямой, заданнойуравнением: 1) y= 1; 2) у = 5; 3) у = -3? если пересекается, то найдитеточку пересечения....

SashaZanevskaya 23.06.2019 22:30

(а+3)^3+(a+1)(a+4) преобразовать в многочлен выражение...

NurBanu1 23.06.2019 22:30

Вычислите, сделав рисунок. sin 135 градусов? sin пи? cos 3пи деленный на 4? cos 180 градусов?...

lalka133722 23.06.2019 22:30

Решите уравнение: 5\7x^9 - 3\14x^9 - 1 1\2x^9 = -1...

narutogovno 23.06.2019 22:30

Уравнение с параметром: найти при каких значениях а уравнение имеет два корня |x+4|\(x+4)=(x+a)^2 пробовала раскрыть модуль по определению и решить, но не получилось могла посчитать...

demeshkin1 23.06.2019 22:30

На автозаправке клиент отдал кассиру 1000- рублей и залили в бак 32 литра бензина по цене 30 руб. 50 копеек за литр. сколько сдачи должен получить клиент? ответ дайте в рублях...

DayanaEstDetei 23.06.2019 22:30

:( ! представьте в виде обыкновенной дроби бесконечную десятичную периодическую дробь: а) 2,(35) б) 1,6(2)...

КсюшаАнтропова 23.06.2019 22:30

Значение переменных х и у таковы, что выполняються равнства х+у=6, ху= -3. найдите значение выражения 1) х3(степень) у2+х2у3...

Доказать, что 4 в восьмой + 2 в тринадцатой делится на 18

Популярные вопросы