До іть будь ласка з вправою на повторення

В решении.

Объяснение:

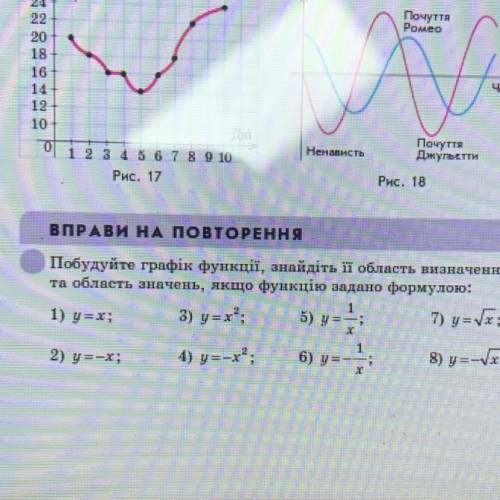
Построить графики функций и найти её область определения.

Область определения - это проекция графика функции на ось Ох, это значения х, при которых функция существует.

Обозначается как D(f) или D(у).

1) у = х;

Таблица:

х   -1     0     1

у    -1     0     1

График - прямая линия, проходящая через начало координат, ничем не ограничена, х может быть любым.

D(у) = х∈R;

2) у = -х;

Таблица:

х   -1     0     1

у    1     0     -1

График - прямая линия, проходящая через начало координат, ничем не ограничена, х может быть любым.

D(у) = х∈R;

3) у = х²

График - классическая парабола с вершиной в начале координат, ветви направлены вверх.

Таблица:

х   -3     -2     -1     0     1     2     3

у    9      4      1      0     1     4     9

Область определения параболы - множество всех действительных чисел, потому что она проецируется на любую точку оси Ох.

D(у) = х∈R;

4) у = -х²

График - классическая парабола с вершиной в начале координат, ветви направлены вниз.

Таблица:

х   -3     -2     -1      0     1     2     3

у   -9     -4     -1      0    -1    -4    -9

Область определения параболы - множество всех действительных чисел, потому что она проецируется на любую точку оси Ох.

D(у) = х∈R;

5) у = 1/х

График - гипербола, расположена в 1 и 3 координатных четвертях.

Таблица:

х   -10       -5     -1     0     1      5     10

у   -0,1    -0,2    -1      -     1    0,2   0,1

Область определения - множество всех действительных чисел, кроме х = 0 (на ноль делить нельзя).

D(у) = х∈R : х ≠ 0;

6) у = -1/х

График - гипербола, расположена во 2 и 4 координатных четвертях.

Таблица:

х   -10      -5     -1     0     1       5       10

у    0,1     0,2     1      -    -1    -0,2    -0,1

Область определения - множество всех действительных чисел, кроме х = 0 (на ноль делить нельзя).

D(у) = х∈R : х ≠ 0;

7) у = √х

Графиком функции y=√x является  ветвь параболы.

Таблица:

х   0     1     4     9

у   0     1     2     3

Область определения - множество всех действительных чисел, только х больше либо равен нулю.

D(у) = х∈R : х >= 0;

8) у = -√х

Графиком функции y = -√x является  ветвь параболы.

Таблица:

х   0     1     4     9

у   0    -1    -2    -3

Область определения - множество всех действительных чисел, только х больше либо равен нулю.

D(у) = х∈R : х >= 0;