Дано : cos альфа= 12/13; 3пи/2 < альфа < 2пи найти: sin альфа; cos (пи/3-альфа)
Ответы
Так как угол в 4 четверти то значение синуса будет <0
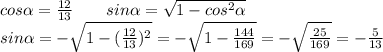
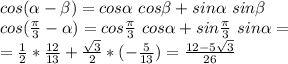
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Популярные вопросы
- В чем проявилось влияние фольклора на пушкинские сказки? Чем сказки...
1 - Расскажите о детстве Уайльда. Что повлияло на развитие его литературного...
3 - Чем понравился придворным искусственный соловей? Почему после того,...
2 - Как относилась вдова к падчерице и собственной дочери? Было такое отношение...
3 - Как Андерсен оценивал свою жизнь? Приведите соответствующие высказывания...
2 - Вы, наверное, заметили, что живой соловей кажется незаметной серой птичьей...
2 - Перечитайте рубрику «Авторитетная цитата. О каких особенностях сказок...
3 - Почему Мальчик-звезда воспитывался в семье Лесоруба? Как он относился...
2 - Чем отличался Мальчик-звезда от своих сверстников? На чем держалась...
1 - Обычно в сказках красота и добро неразделимы: красивые персонажи имеют...
2