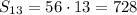Дана последовательность двузначных натуральных чисел, кратных 7: а) составить формулу n-ого члена последовательности б) найти сумму членов последовательности
Другие вопросы по теме Алгебра
Популярные вопросы
- 1. Брусок №1 массой 3 кг налетает на неподвижный брусок №2 массой...
1 - В треугольнике АBC AC = BC, угол C равен 50 0 . Найдите внешний...
1 - 4 * Label the plctures.• stormy sej • poor •nch • servants• clouds...
1 - 8.-тапсырма. «Мамандық таңдау — жасөспірім шақтағы ең маңызды шешімдердің...
1 - Самопознание 5 класс Творческая деятельность, групповая работа....
1 - 3 бутил циклобутан структурная формула...
2 - Дайте характеристикому источнику: группа Фото-видео материалы...
2 - Учебные задания УСПЕХОВ! 1.Знать содержание учебного материала.2.Прочитать...
1 - Ss the Curriculum 6f 7.56 Which of the types of media below do...
2 - 4.×84×7 - 7гулять на свежем воздухе какой ответ...
3
имеется последовательность двузначных натуральных чисел, кратных 7:
14; 21; ... ; 98 - арифметическая прогрессия с первым членом 14 и разностью прогрессии d=7
a)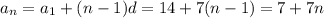 , n = 1,...,13.
, n = 1,...,13.
Всего таких двузначных чисел: 13
b)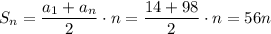
Поскольку таких двузначных чисел n=13, то