Дана функция f(x)=x^3+6x^2+7x-2 напишите уравнение касательной к графику функции y=f(x) параллельной прямой y=-2x+7​

Производная данной функции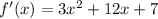

Пусть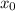 - абсцисса точки касания прямой к кривой.

Известно, что неизвестная прямая(касательная) параллельна прямой y = -2x + 7, следовательно, у них угловые коэффициенты равны: k = -2.

По геометрическому смыслу производной, мы имеем:

По теореме Виета получаем и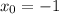

Т.е. имеет две касательные к данной кривой. Найдем их.

Общий вид уравнения касательной: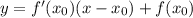

Подсчитаем значение функции и значение производной функции в точке

Уравнение касательной: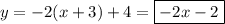

Аналогично, подсчитаем значение функции и значение производной функции в точке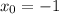

Уравнение касательной: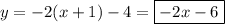

P.S. Можно было не считать значения производной функции, поскольку это и есть угловой коэффициент k = -2.