Дана арифметическая прогрессия 35,32, найдите первый отрицательный член этой прогрессии решение
Другие вопросы по теме Алгебра
Популярные вопросы
- Чем знаменателен в изучении земли хх век...
2 - Ин яз 5 класс. нужно поставить слова в правильном времени. the...
2 - Напишите о человеке с внутренней дисциплиной...
2 - Часы показывают 20 часов 22 минуты. какое время они показывали...
1 - По 20 составить 5 предложений на со словами a break, compulsory...
2 - Сочинение на тему почему владимир дубровский стал разбойником по...
2 - Составить 2 группы предложений в 1 группу 2 предложения в 2 группу...
2 - Решить уравнение! 5(x-9)=-2 9(x+7)=-7 заранее !...
1 - Одна третья часть 96 учеников учиться в 3а классе, а остальные...
1 - Який механізм розвитку інфаркта міокарда?...
3
Арифметическая прогрессия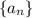 . a₁=35; a₂=32; a₃=29
. a₁=35; a₂=32; a₃=29
Разность арифметической прогрессии d = a₂-a₁=32-35=-3
Формула n-го члена арифметической прогрессии
35 - 3 (n - 1) < 0
35 - 3n + 3 < 0 ⇔ 3n > 38 ⇔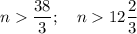
Первый отрицательный член прогрессии - тринадцатый.
n = 13 ⇒ a₁₃ = a₁ + d(13-1) = 35 - 3·12 = -1
ответ: a₁₃ = -1