1. Алгебра
  2. Дан многочлен P(x) с целыми

Дан многочлен P(x) с целыми коэффициентами. P(5) делится на 2, P(2) делится на 5. Докажите, что P(7) делится на

teddy33 teddy33    1   06.06.2021 12:33    7

Ответы
laconee97 laconee97  06.07.2021 12:34

Объяснение:

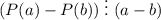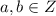Согласно теореме Безу (P(a)-P(b))\;\vdots\;(a-b), где a,b\in Z.

Значит,

(P(7)-P(5))\;\vdots\;(7-5)=2 . Так как, по условию, P(5)\;\vdots\;2, то P(7)\;\vdots\;2;(P(7)-P(2))\;\vdots\;(7-2)=5 . Так как, по условию, P(2)\;\vdots\;5, то P(7)\;\vdots\;5.

Тогда, так как числа 2 и 5 взаимно просты,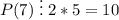 P(7)\;\vdots\;2*5=10.

Что и требовалось доказать.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
asarapik asarapik  18.09.2019 06:30
Пользуйся таблицей квадратов двузначных чисел вычислите 1) -0,2*√7,84-1/3*√10,89 2) 3*1/√81-1/4*√256 если что ответ должен получиться (1) -1,66 (2) -3 целых 2/3...
St1ler St1ler  18.09.2019 08:10
Есть 987654321 можно ставить где угодно - и + но надо получить 500...
Аааааяяяяяннннн Аааааяяяяяннннн  18.09.2019 08:10
Найдите значение выражения -5x^3+y^2 если x=-10 а y=11...
солнышко279 солнышко279  18.05.2021 17:49
) раза. Вопрос такой- с какой вероятностью ДВАЖДЫ выпадет Тройной дубль на костях. Пример такого выпадения: 111- первый бросок 333- второй бросок 456- третий бросок...
Zyherpopentruher007 Zyherpopentruher007  18.05.2021 17:49
В парке при музее решили разбить клумбу в форме четырёхугольника. Две стороны этой клумбы (AD и BC), если бы можно было продлить их на бесконечную длину, никогда...
ХудшийИзХудших ХудшийИзХудших  18.05.2021 17:49
, очень нужно, обязательно решение должно быть..​...
serhio2000 serhio2000  18.05.2021 17:50
мне порешать задачу на: Побудувати графік функції y=x²+2x-8 , же!)))...
Rasul101231 Rasul101231  18.05.2021 17:50
мне порешать эту задачу на Знайдіть область визначення функції: 1). f(x)=√x+4+2/x+1; 2). f(x)=√8-x+4/x²-8x , же!)))...
maruya3 maruya3  06.05.2021 06:40
1) Сократить дроби: a) 16x^ 3 80x^ 7 = б) y+3 y2-9= в) x ^ 2 - 2xy + y ^ 2 * x - y = 2) выполните умножение и деление алгебраических дробей: a) 122a*5a27= б) 153ху...
Annkeklol Annkeklol  05.08.2019 19:40
Вычисли корень уравнения 7,4⋅c=25,9...

Популярные вопросы