Чи можна подати число √2+1 у вигляді арифметичного квадратного кореня з якогось раціонального числа? Очень
Другие вопросы по теме Алгебра
Популярные вопросы
- Дана система двух линейных уравнений:{y+9x=22y−9x=4...
3 - Назовите по описанию сказку. Я просто забыл название. ремесленик...
2 - Який опір має відрізок мідної проволоки завдовжки 2 км, якщо радіус...
2 - Чим відрізнялося управління Новгорода від управління інших князівств?...
3 - ОЧЕНЬ ! Можно ли назвать эксперимент профессора Преображенского нравственным?...
3 - какое значение имеет изучение географического положения и других...
3 - На 10000 жителів припадав 1 учень на а) 150 чол б) 100 чол в ) 50...
1 - Какая листовая пластика у семейства бобовых (мотыльковых) ?...
1 - Напишіть три речення з одиничним невідокремленим дієприслівником....
1 - 1time in the sun is good for you, but no more than 15 minutes. 2...
1
Допустим, что число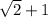 - результат извлечения квадратного корня из некоторого рационального числа - обозначим его буквой
- результат извлечения квадратного корня из некоторого рационального числа - обозначим его буквой 
Тогда можем записать:
Если данное уравнение имеет рациональное решение, то число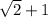 таки можно представить в виде корня из рационального числа.
таки можно представить в виде корня из рационального числа.
Обе части возведем в квадрат (учтем, что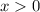 . Очевидно, что
. Очевидно, что 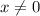 .
.
Имеем: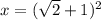
Правую часть распишем как квадрат суммы:
Однако полученное числа не является рациональным. Значит, ответ - нет.