Часть А
А1. Укажите, какое число является корнем уравнения 3х – 2 = х + 4
А2. Вычислите: 24- 23 (2 в 4 степени; 2 в 3 степени)
А3.У выражение: 4n2 · 0,2n5
А4. Выполните умножение: (2а – 7в)(7в + 2а).
Часть В
В1. ( ) У выражение: а(3а + 2b) – b(2a – 5b)
В2.( ) Функция задана формулой у = 0,5х – 7,1. При каком значении аргумента значение функции равно – 5, 4.
Часть С
С ( ). Решите уравнение: (х – 2)2 + 3х – 6 – 5(2 – х) = 0.
Другие вопросы по теме Алгебра
Популярные вопросы
- 1) точка к принадлежит отрезку ав длиной 3 м и делит его в отношении...
1 - Произведение равно 39 . какими могут быть первый и второй множители ?...
1 - В10 л сока 60% чистого фруктового экстракта. сколько фруктового экстракта...
2 - Впрямоугольном треугольнике катеты равны 20 сантиметров и 15 сантиметров...
3 - Краткое содержание храбрость 5 6 предложений...
1 - Два пешехода одновременно отправились из пункта c в противоположные стороны...
1 - Найдите сумму значений t или значение t если оно единственное, при котором...
1 - Стоимость проездного на месяц - 800 руб. а стоимость 1 поездки - 22 руб....
2 - Масова частка гідрогену в кристалогідраті складу меso4 умножить 6н2о...
1 - Найти значение cos6α, если sin2α=√3/2, α∈[0; π/4]...
2
A1: x=3
A2: 8
A3: 0,8
A4: 4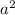 - 49
- 49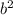
В1:3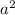 + 5
+ 5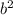
B2: 4,2 | 22,2
С: x = 2
Объяснение:
A1:
3x - 2 = x + 4
2x = 6
x =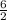 = 3
= 3
A4:
(2a - 7b)*(2a + 7b) = 4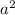 - 49
- 49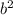 (Формула сокр. умножения)
(Формула сокр. умножения)
B1:
а(3a + 2b) – b(2a – 5b) = 3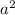 + 2ab - 2ab + 5
+ 2ab - 2ab + 5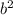 = 3
= 3
B2:
у = 0,5x – 7,1
1) -5 = 0,5x - 7,1; 2,1 = 0,5x; x = 4,2:
2) 4 =0,5x - 7,1; 11,1 = 0,5x; x = 22,2
C:
(x – 2)2 + 3x – 6 – 5(2 – x) = 0
2x - 4 +3x - 6 - 10 + 5x = 0
10x = 20
x = 2
A2:
A3:
4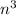 * 0,2
* 0,2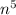 = 0,8
= 0,8 (4*0,2 и сложение степеней n)
(4*0,2 и сложение степеней n)